We now turn our attention to Fourier series, which, not unlike power series, allows us to represent periodic functions in terms of an infinite series.
Definition:
Let
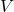
be a vector space over the complex numbers. Then, an
inner product (sometimes called a
Hermitian product) on
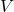
is a map
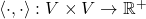
such that
- (Positive definitieness)
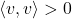 if and only if
if and only if 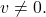
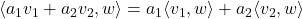 for all
for all 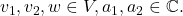
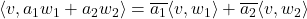 for all
for all 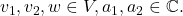
In other words, the inner product is linear in the first argument and conjugate-linear in the second argument. If
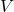
admits an inner product,
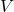
is called an
inner product space.
Remark:
Note that an inner product on
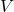
defines a norm on
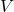
by
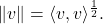
Definition:
A complete inner product space is called a
Hilbert space.
Proposition (Cauchy-Schwarz):
If
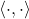
is an inner product on
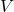
and

is a norm on
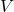
induced by the inner product, then

for all
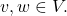
Proof:
The proof of Cauchy-Schwarz was part of homework 1.
Definition:
Let
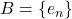
be a linearly independent set in a Hilbert space
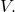
Then,
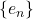
is called an
orthonormal basis if every
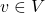
can be written in the form
![Rendered by QuickLaTeX.com \[v = \sum_B a_n e_n\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cf53765975152b9d146b59c088801a93_l3.png)
for some coefficients
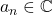
(i.e.
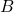
spans
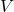
), and

when
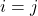
and
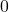
otherwise.
Remark:
Note that this implies that
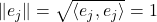
for all
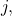
i.e.
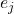
are unit vectors.
Remark:
Note that this is different from a regular basis for a vector space, as infinitely many terms are allowed in the sum. This is where the assumption of completeness is necessary, also creating an issue regarding the question of whether the sum
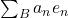
is well-defined (since it can have infinitely many terms), but it turns out that if an orthonormal basis exists, then there are at most countably many terms in the sum, which lets it take the form
![Rendered by QuickLaTeX.com \[\sum_{j=1}^\infty a_n e_j\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-317768aaf5ad5a7bebd251446684ad8b_l3.png)
after rearranging the basis elements
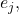
which can be well-defined in terms of convergence of partial sums.
Example:

with the Hermitian product
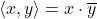
is a Hilbert space with orthonormal basis

Proposition (Pythagorean Theorem):
If
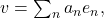
then
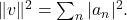
Proof:
Calculate
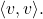
Proposition:
If
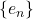
is an orthonormal basis for

then

can be written uniquely as
![Rendered by QuickLaTeX.com \[v = \sum_{B} \langle v,e_n \rangle e_n.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-00e1af5212b32af3346edc7d4808daeb_l3.png)
Proof:
By the Pythagorean theorem, if
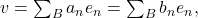
then
![Rendered by QuickLaTeX.com \[\left\|\sum_B (a_n-b_n) e_n \right\| = \sum_B (a_n-b_n)^2 = 0,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-c3fb8a4222e819236609149266734ac0_l3.png)
i.e.

for all
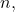
so the decomposition is unique. It is left to verify that this sums equals
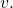
Indeed, if
![Rendered by QuickLaTeX.com \[v= \sum_n a_n e_n,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-d5e0276ffb0f070024ec4013c2da0ef5_l3.png)
since the
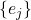
are orthonormal,
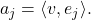
Thus,
![Rendered by QuickLaTeX.com \[v = \sum_{B} \langle v, e_n \rangle e_n,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-32f5b99c08e0ff594574b1e4f75fd66d_l3.png)
which yields the desired equality.
Corollary (Parseval’s Identity):
![Rendered by QuickLaTeX.com \[\sum_{n} |\langle v, e_n \rangle|^2 = \|v\|^2.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-826b3d94218f1af7606bc0f43e0ee363_l3.png)
Proof:
Follows immediately from the Pythagorean theorem.
Now, consider the vector space of complex-valued periodic functions with period 1, denoted
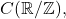
with the inner product given by
![Rendered by QuickLaTeX.com \[\langle f, g \rangle = \int_0^1 f(x) \overline{g(x)} dx.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-d17a78d967bc27b12249eb37024e4aec_l3.png)
One easily checks that this is indeed an inner product, which induces the
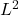
norm on
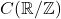
given by
![Rendered by QuickLaTeX.com \[\|f\|_{L^2} = \left(\int f(x)^2 dx\right)^{\frac{1}{2}},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-961bc88bcebc41b12abfe14c0f2b5a50_l3.png)
which in turn induces the
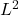
metric. One says
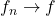
in
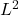
if
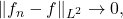
or equivalently,
![Rendered by QuickLaTeX.com \[\left(\int_0^1 (f_n(x)-f(x))^2 dx\right)^{\frac{1}{2}} \to 0.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cf23902fc29c83daae100f40540c3922_l3.png)
Definition:
Define
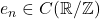
to be
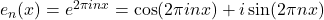
for
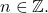
A sum of the form
![Rendered by QuickLaTeX.com \[\sum_{k=-n}^n a_n e_n,a_n \in \mathbb{C},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-feb29698dbad428f79e529001488894c_l3.png)
is called a
trigonometric polynomial.
We now ask a question that comes from linear algebra: does there exist an orthonormal basis for
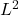
? To answer the following question, one requires the following important theorem:
Theorem (Weierstrass Approximation Theorem):
Trigonometric polynomials are dense in
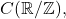
or equivalently, for any
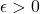
and
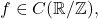
there exists a trigonometric polynomial
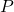
such that
![Rendered by QuickLaTeX.com \[\|f-P\|_{L^2} < \epsilon.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f9e0ed547a7737b2c7a29846762237ff_l3.png)
Proof:
Unfortunately, we do not have time to prove this theorem, but it relies on an important concept known as an approximation to the identity.
We are now able to prove our main result:
Theorem:
Then,
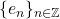
is an orthonormal basis for
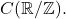
Proof:
Indeed,
![Rendered by QuickLaTeX.com \[\int_0^1 e^{2\pi i nx} \overline{e^{2\pi i mx}}dx = \int_0^1 e^{2\pi i (n-m) x} dx = 1 \text{ when } n=m, 0 \text{ otherwise}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-943ea6d259bdc9b09663f271a83984b6_l3.png)
Finally, one needs to show that
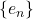
spans
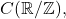
i.e. every periodic function with period 1 can be represented as a (possibly infinite) sum of sines and cosines. We claim that for any
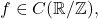
![Rendered by QuickLaTeX.com \[f=\sum_{n=-\infty}^\infty \langle f,e_n \rangle e_n = \sum_{n=-\infty}^\infty \left(\int_0^1 f(y) e^{-2\pi i ny} dy\right) e^{2\pi i nx}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-1b04964be64bb709c052005bb757c9a5_l3.png)
Since
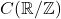
has the
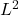
norm, we need to show that the partial sums converge
![Rendered by QuickLaTeX.com \[f_k = \sum_{n=-k}^k \langle f,e_n\rangle e_n \to f\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5acd27adfa3afd451673087475452dc9_l3.png)
in
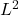
norm as
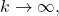
or equivalently,
![Rendered by QuickLaTeX.com \[\int_0^1 (f(x)-f_k(x))^2 dx \to 0.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-92418b37009b2e73c91d601a55e01459_l3.png)
By the Weierstrass Approximation Theorem, pick a trigonometric polynomial

such that
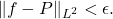
Now, note that for any

![Rendered by QuickLaTeX.com \[\left\langle f-\sum_{n=-k}^k \langle f, e_n \rangle, e_m\right\rangle = 0\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-596ba103a529a34f6fccdf788532aa5e_l3.png)
for sufficiently large
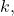
so by linearity of the inner product,
![Rendered by QuickLaTeX.com \[\left\langle f-f_k, P-f_k\right\rangle=0.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ba21b011413daad9e695b5c6f8418baf_l3.png)
Then, by the Cauchy-Schwarz inequality, we get
![Rendered by QuickLaTeX.com \[\|f-f_k\|_{L^2}^2=\langle f-f_k, f-f_k\rangle= \langle f-f_k,f-P\rangle + \langle f-f_k, P-f_k\rangle \leq \|f-f_k\|_{L^2}\epsilon,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-92feba23559877549e574a83e6701955_l3.png)
so
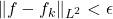
for any
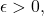
completing the proof.
Definition:
The coefficients of the basis elements
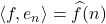
are called the
Fourier coefficients of
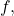
and the function
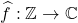
is called the
Fourier transform of
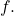
Corollary (Plancherel’s Theorem):
![Rendered by QuickLaTeX.com \[\sum_n |\widehat{f}(n)|^2 = \int_0^1 f(x)^2dx \Longleftrightarrow \|\widehat{f}\|_{l^2}=\|f\|_{L^2}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-51fdffd06631e2aa6c762eb0d00ea511_l3.png)
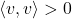 if and only if
if and only if 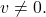
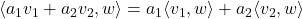 for all
for all 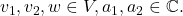
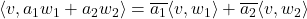 for all
for all 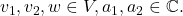
![]()
![Rendered by QuickLaTeX.com \[\sum_{j=1}^\infty a_n e_j\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-317768aaf5ad5a7bebd251446684ad8b_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\left\|\sum_B (a_n-b_n) e_n \right\| = \sum_B (a_n-b_n)^2 = 0,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-c3fb8a4222e819236609149266734ac0_l3.png)
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\left(\int_0^1 (f_n(x)-f(x))^2 dx\right)^{\frac{1}{2}} \to 0.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cf23902fc29c83daae100f40540c3922_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=-n}^n a_n e_n,a_n \in \mathbb{C},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-feb29698dbad428f79e529001488894c_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[f_k = \sum_{n=-k}^k \langle f,e_n\rangle e_n \to f\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5acd27adfa3afd451673087475452dc9_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\left\langle f-\sum_{n=-k}^k \langle f, e_n \rangle, e_m\right\rangle = 0\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-596ba103a529a34f6fccdf788532aa5e_l3.png)
![]()
![]()
![]()