Easy:
- Prove the parallelogram law: for any inner product space
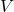 and
and 
![Rendered by QuickLaTeX.com \[\|x+y\|^2 + \|x-y\|^2 = 2\|x\|^2 + 2\|y\|^2.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-7d036fc816abd015d065a30a80adca32_l3.png)
- Show that the space
is a Hilbert space.![Rendered by QuickLaTeX.com \[l^2(\mathbb{C}) = \{(x^n)_{n=1}^\infty, x_n \in \mathbb{C}: \langle (x^n), (x^m) \rangle = \sum_{i=1}^\infty x^{n}_i \overline{x^m_i} < \infty\}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9a3a709951e5dc4829a09f8a80ea16cf_l3.png)
- Give an example of an inner product space that is not a Hilbert space, i.e. an inner product space that is not complete.
- If
 converges to
converges to 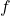 in
in 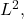 does it converge uniformly? Prove the statement or find a counterexample.
does it converge uniformly? Prove the statement or find a counterexample.
Intermediate:
- Let
 Show that all partial derivatives of
Show that all partial derivatives of 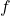 exist at
exist at  but that
but that 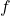 is not differentiable at
is not differentiable at  Explain why these two facts do not contradict each other.
Explain why these two facts do not contradict each other. - Show that if
 is has a continuous derivative
is has a continuous derivative 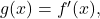 then
then  in other words, the Fourier transform turns differentiation into multiplication.
in other words, the Fourier transform turns differentiation into multiplication. - For
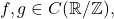 define the convolution
define the convolution
Show that![Rendered by QuickLaTeX.com \[(f * g)(x) = \int_0^1 f(x-y) g(y) dy.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-481f109b82672456374f1ccc08c6dab9_l3.png)
![Rendered by QuickLaTeX.com \[\widehat{f * g}(n) = \widehat{f}(n)\widehat{g}(n).\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ee64f5ead8b9156854a9b005abc84470_l3.png)
Challenging:
- Use the Fourier transform to solve the differential equation
(Hint: use problem 6).![Rendered by QuickLaTeX.com \[u''+4\pi^2 u=0,u(0)=u(1).\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-c5c77a5639cd962281ef5dc31b2a71e4_l3.png)
- Let
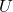 be a neighborhood of
be a neighborhood of 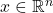 and let
and let 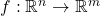 be continuous with continuous first order partial derivatives on
be continuous with continuous first order partial derivatives on 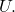 Show
Show 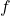 is differentiable at
is differentiable at 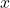 and
and  is given by the Jacobian matrix.
is given by the Jacobian matrix.