This week, we will talk a lot about power series over
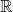
and
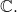
The Weierstrass M-Test, which was proven last time, is what will help us take advantage of power series expansions of analytic functions. To understand the full power of power series, it is extremely useful to deal with complex quantities,
so we begin with a brief review of complex numbers.
Definition:
For
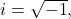
define the
complex numbers 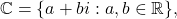
with elementary operations given by
![Rendered by QuickLaTeX.com \[(a+bi) \pm (c+di) = (a+c) \pm (b+d)i, (a+bi)(c+di) = (ac-bd)+(ad+bc)i,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cfb4a8b2a16f33932541fe6656736dfc_l3.png)
and
![Rendered by QuickLaTeX.com \[\frac{a+bi}{c+di} = \frac{a+bi}{c+di} \cdot \frac{c-di}{c-di} = \frac{(ac+bd) + (bc-ad)i}{c^2+d^2}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-bfbb9ab7955118ff75b34b56f76166e7_l3.png)
For a complex number
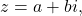
define the
real and complex parts 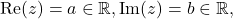
i.e.
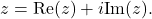
Moreover, define the
conjugate 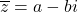
and the
absolute value 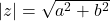
(which defines a norm and therefore a metric on
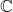
). Note the identity

Remark:
Note that the complex numbers are equivalent (isomorphic) as a metric space to the list of tuples
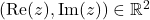
with the
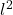
metric. Thus,
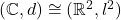
as metric spaces.
Recall that complex numbers can be represented in polar form
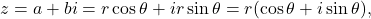
where
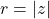
and
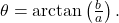
By using the multiplication rules for complex numbers and trig identities for the sine and cosine of a sum of angles, one recognizes that
![Rendered by QuickLaTeX.com \[r_1 (\cos \theta_1 + i \sin \theta_1) (\cos \theta_2 + i \sin \theta_2) = r_1 r_2 (\cos (\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)).\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-329659025b60d1942025fe5d95e4d91d_l3.png)
Motivated by this, we introduce
Euler’s notation for complex numbers
![Rendered by QuickLaTeX.com \[z = r(\cos \theta+i \sin \theta) =re^{i \theta}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5827378ea4b497b8bceb39072da9a169_l3.png)
Then, one easily checks that
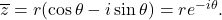
Similarly, to real functions

one can define complex-valued functions
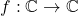
taking values in the complex numbers. One can thus also take derivatives of continuous complex functions by treating

as a variable, e.g.
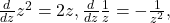
etc.
We are now able to approach power series in full generality.
Definition:
A
complex power series centered around 
is an expression of the form
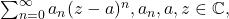
which can be operated on using
![Rendered by QuickLaTeX.com \[\sum_{n=0}^\infty a_n (z-a)^n + \sum_{n=0}^\infty b_n (z-a)^n = \sum_{n=0}^\infty (a_n+b_n) (z-a)^n\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5c5c196c8cad86ce0e54fc5da2a98ec9_l3.png)
and
![Rendered by QuickLaTeX.com \[\sum_{n=0}^\infty a_n (z-a)^n \times \sum_{n=0}^\infty b_n (z-a)^n = \sum_{n=0}^\infty \left(\sum_{k=0}^n a_k b_{n-k}\right) (z-a)^n.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-a79f0e89aeb94027a3d3712c0a3b39c4_l3.png)
If

is a real number, the power series is called a real power series.
Remark:
Convergence of complex power series relies heavily on one of the convergence tests covered in 131A, namely, the Absolute Convergence Test, which states that if
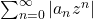
converges, then
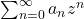
converges.
Proposition:
Suppose
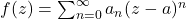
is a complex power series. Then, if the power series converges for at least one

such that
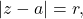
then it converges absolutely for
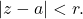
Proof:
Suppose
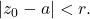
Then, since
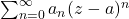
converges,

so in particular, the terms of the sum are bounded. Suppose
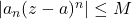
for some

Then,
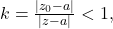
so
![Rendered by QuickLaTeX.com \[|a_n(z_0-a)^n| = |a_n| (k|z-a|)^n\leq Mk^n,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9bdccd39c61b696f6bb4bbf47cb531ff_l3.png)
which gives a convergent geometric series since
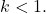
Thus, by the Absolute Convergence Test, the series converges absolutely for
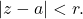
Definition:
Define the
radius of convergence of a power series

Then, the power series converges for
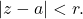
Example:
The familiar geometric series
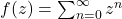
converges for
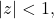
since
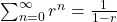
for
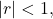
showing that

on the open unit ball

in the complex plane.
Remark:
Note that the radius of convergence
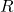
defines an open ball
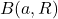
on which the series converges. By definition, the series diverges for

but on the boundary
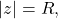
one has to use other techniques to determine whether the power series converges or diverges. For instance, in the previous example, for
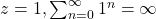
diverges.
Definition:
For a sequence
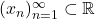
of real numbers, we define the
limit superior and
limit inferior to be
![Rendered by QuickLaTeX.com \[\limsup_{n \to \infty} a_n = \lim_{n \to \infty} \sup_{k \geq n} a_n\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-379a46cb139fb7249f02aa41539f0361_l3.png)
and
![Rendered by QuickLaTeX.com \[\liminf_{n \to \infty} a_n = \lim_{n \to \infty} \inf_{k \geq n} a_n.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-dddbc289b0d505cd0ecb9e75f32282ee_l3.png)
Proposition:
If
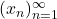
is a sequence of real numbers,
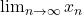
exists if and only if
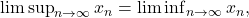
in which case
![Rendered by QuickLaTeX.com \[\limsup_{n \to \infty} x_n = \liminf_{n \to \infty} x_n = \lim_{n \to \infty} x_n.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5128ff8330e2d6b82e87ef4572a9c289_l3.png)
Proof:
Exercise.
Proposition:
The radius of convergence of a power series
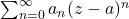
is given by
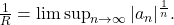
Proof:
We compare the series to a geometric series, which we know converges for
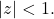
We thus want
![Rendered by QuickLaTeX.com \[\sum_{n=0}^\infty |a_n z_n| = \sum_{n=0}^\infty (|a_n|^{\frac{1}{n}}|z|)^n \leq \sum_{n=0}^\infty r^n<\infty,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-3402b1d5fd7f49cb23624301a3e8fdfc_l3.png)
which converges for
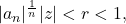
or equivalently, for
![Rendered by QuickLaTeX.com \[\frac{1}{|z|}>\frac{1}{|a_n|^{\frac{1}{n}}}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-13c51a4edfbc0a56435b5f4e31169435_l3.png)
Since this has to be true as
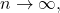
one has to take the
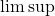
on both sides. Set
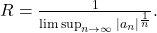
One notes that for
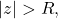
comparison with a geometric series yields
![Rendered by QuickLaTeX.com \[\infty = \sum_{n=0}^\infty |a_n (R+\epsilon)^n|\leq \sum_{n=0}^\infty |a_n z^n|,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-4f0b0df35bd82ddc87e015662641c36d_l3.png)
so the series diverges for
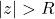
and converges for
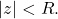
Thus,
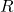
is the radius of convergence.
Another convergence test often comes in handy.
Proposition (Ratio Test):
The radius of convergence of

is
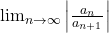
if the value of the limit exists.
Proof:
Exercise.
One notes that in the example above we were able to define a continuous function using a power series. One question to ask is when is the function defined by a power series continuous. The answer comes by using the Weierstrass M-Test.
Proposition:
Suppose

is a power series with radius of convergence
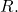
Pick
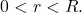
Then, if
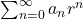
converges, the power series converges uniformly to a continuous function

on

Proof:
Clearly,
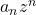
is a continuous function with
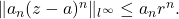
Thus, an application of the Weierstrass M-Test immediately yields the result.
Remark:
This proposition implies that on any closed ball contained inside
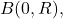
where
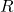
is the radius of convergence of the power series, a power series defines a continuous function
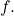
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\sum_{n=0}^\infty a_n (z-a)^n \times \sum_{n=0}^\infty b_n (z-a)^n = \sum_{n=0}^\infty \left(\sum_{k=0}^n a_k b_{n-k}\right) (z-a)^n.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-a79f0e89aeb94027a3d3712c0a3b39c4_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
![]()