This week, we will discuss the notions of pointwise and uniform convergence.
Definition:
A sequence of functions
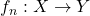
between metric spaces is said to
converge pointwise to a function

if
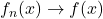
in
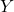
for all

Definition:
A sequence of functions
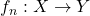
defines a metric space

with the metric of uniform convergence
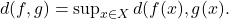
Then, a sequence
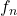
is said to
converge to  uniformly
uniformly if
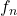
converge to

in

with the uniform convergence metric; that is, for every
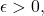
there exists an
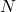
such that
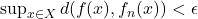
for

Examples:
- If
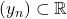 is a convergent sequence of real numbers,
is a convergent sequence of real numbers,  then the constant functions
then the constant functions 
 converge uniformly to
converge uniformly to 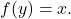
- The sequence
![Rendered by QuickLaTeX.com f_n:[0,1] \to \mathbb{R}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-dad2ee6674e819fe9cfb90924792dbc9_l3.png) defined by
defined by  converges pointwise to
converges pointwise to 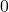 for
for  and
and 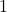 for
for  since
since  for
for  and
and 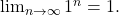 But,
But, ![Rendered by QuickLaTeX.com \[d(f_n,0) = \sup_{x \in [0,1]} |x^n| = 1,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-240fed78f500500bee37d1c38ada3a47_l3.png)
so  uniformly.
uniformly.
While it is true that uniform convergence implies pointwise convergence, the preceding example shows that pointwise convergence does not necessarily imply uniform convergence.
Uniform convergence is a lot more powerful because it preserves continuity.
Proposition:
If
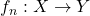
is a sequence of continuous functions that converges uniformly to some function
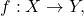
then

is continuous.
Proof:
Let

Then, there exists an
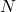
and a
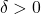
such that
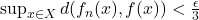
and
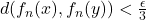
whenever
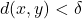
and

Then, by the triangle inequality,
![Rendered by QuickLaTeX.com \[d(f(x),f(y)) \leq d(f(x),f_n(x)) + d(f_n(x),f_n(y)) + d(f_n(y),f(y)) < \frac{\epsilon}{3} + \frac{\epsilon}{3} + \frac{\epsilon}{3} = \epsilon\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-6de13ebb8958924da483c8fe330a6571_l3.png)
whenever
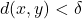
and
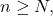
showing that

is continuous.
Corollary:
For any metric space
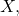
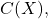
the space of continuous functions on
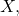
is closed in the space
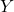
of all functions.
The name for uniform convergence comes from the fact that it does not depend at the point of the domain that one chooses. This lets us similarly define another uniform property – uniform continuity.
Definition:
A function

is
uniformly continuous if for every
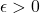
there exists a
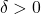
independent of
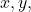
such that for all
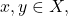
if
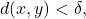
then

Examples:
 given by
given by  is uniformly continuous, since for any
is uniformly continuous, since for any 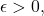
 is such that
is such that 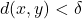 implies
implies 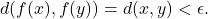
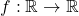 given by
given by  is not uniformly continuous. This can be seen as for any
is not uniformly continuous. This can be seen as for any 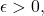 one can find a
one can find a 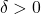 such that
such that  whenever
whenever  only if
only if  for some fixed
for some fixed 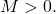 But since the domain is
But since the domain is 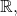 such a
such a  must necessarily depend on
must necessarily depend on 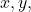 showing that
showing that  is not uniformly continuous.
is not uniformly continuous.
Proposition:
A continuous function on a compact metric space is uniformly continuous.
Proof:
Exercise.
Definition:
For a function
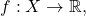
define the
supremum norm of

to be
![Rendered by QuickLaTeX.com \[\|f\|_\infty = d(f,0) = \sup_{x \in X} f(x).\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-d22c4cf42ff667278eecfce953ffd902_l3.png)
Theorem (Weierstrass M-Test):
Suppose
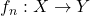
is a sequence of bounded continuous functions such that

converges. Then, the function

defined by
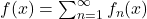
is continuous, and the sum converges uniformly to
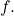
Proof:
Since
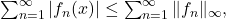
and the latter sum converges, the former sum is absolutely convergent, so by the Absolute Convergence Test,
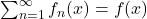
exists. Define
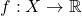
pointwise by
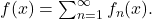
It remains to show that

is continuous, for which we use the fact that the limit of a uniformly convergent sequence of functions is continuous. We see by the triangle inequality that
![Rendered by QuickLaTeX.com \[d\left(f,\sum_{n=1}^k f_n\right) = \sup_{x \in X} \left|\sum_{n=1}^\infty f_n(x) - \sum_{n=1}^k f_n(x) \right| = \sup_{x \in X} \left|\sum_{n=k+1}^\infty f_n(x) \right| \leq \sum_{n=k+1}^\infty \|f_n\|_\infty < \epsilon\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ef0e464399701608a013c008dd9d1a75_l3.png)
for sufficiently large
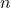
since by assumption, the sum converges. Thus,
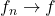
converges uniformly, and since each
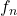
is continuous,

is continuous.
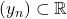 is a convergent sequence of real numbers,
is a convergent sequence of real numbers,  then the constant functions
then the constant functions 
 converge uniformly to
converge uniformly to 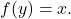
![Rendered by QuickLaTeX.com f_n:[0,1] \to \mathbb{R}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-dad2ee6674e819fe9cfb90924792dbc9_l3.png) defined by
defined by  converges pointwise to
converges pointwise to 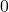 for
for  and
and 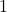 for
for  since
since  for
for  and
and 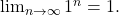 But,
But, ![Rendered by QuickLaTeX.com \[d(f_n,0) = \sup_{x \in [0,1]} |x^n| = 1,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-240fed78f500500bee37d1c38ada3a47_l3.png)
 uniformly.
uniformly.![]()
 given by
given by  is uniformly continuous, since for any
is uniformly continuous, since for any 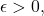
 is such that
is such that 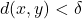 implies
implies 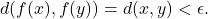
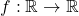 given by
given by  is not uniformly continuous. This can be seen as for any
is not uniformly continuous. This can be seen as for any 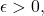 one can find a
one can find a 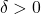 such that
such that  whenever
whenever  only if
only if  for some fixed
for some fixed 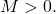 But since the domain is
But since the domain is  such a
such a  must necessarily depend on
must necessarily depend on 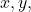 showing that
showing that  is not uniformly continuous.
is not uniformly continuous.![]()
![Rendered by QuickLaTeX.com \[d\left(f,\sum_{n=1}^k f_n\right) = \sup_{x \in X} \left|\sum_{n=1}^\infty f_n(x) - \sum_{n=1}^k f_n(x) \right| = \sup_{x \in X} \left|\sum_{n=k+1}^\infty f_n(x) \right| \leq \sum_{n=k+1}^\infty \|f_n\|_\infty < \epsilon\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ef0e464399701608a013c008dd9d1a75_l3.png)