Contraction Mapping and Connectedness
Before talking about continuity, I wanted to discuss a very important result regarding compactness known as the contraction mapping theorem:
Theorem (Contraction Mapping Theorem):
Let

be a complete metric space, and

be a contraction, i.e.
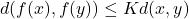
for some
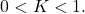
Then,

has a unique fixed point
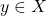
such that

Proof:
Our goal is to construct a Cauchy sequence. Define
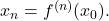
Then,
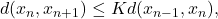
so iterating yields
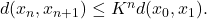
Moreover, by the triangle inequality and the geometric series formula, one obtains
![Rendered by QuickLaTeX.com \[d(x_n,x_m) \leq (K^n + K^{n+1}+... + K^{m-1}) d(x_0,x_1) = K^n(1 + K + ... +K^{m-1}) d(x_0,x_1) \leq \frac{K^n}{1-K} d(x_0,x_1) \to 0\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-94e48c6758bae82da3dbc9e5ddf8bf81_l3.png)
as
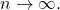
Thus, the sequence is Cauchy, so it has a limit
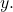
But then,
![Rendered by QuickLaTeX.com \[f(y) = f(\lim_{n \to \infty} x_n) = \lim_{n \to \infty} f(x_n) = \lim_{n \to \infty} x_{n+1} = y,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ec899009011ef3777098b02156ec2e79_l3.png)
so
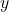
is a fixed point of
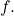
If there were two fixed points
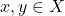
then
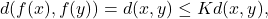
which is a contradicton, so uniqueness follows.
Example:
When using a calculator, when you press

many times and enter some number in radians, you will always get a value very close to
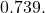
Why? Well, suppose one lets
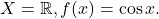
Then, by the mean value theorem,
![Rendered by QuickLaTeX.com \[\frac{|\cos(x)-\cos(y)|}{|x-y|} = |\sin(x')| \leq 1,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-1a43267957d0404c6b52b6a0be01792e_l3.png)
i.e.
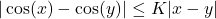
for

Then only thing left to show is that
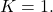
We know
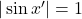
only when

so let’s consider the interval
![Rendered by QuickLaTeX.com [-1,1].](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-7e4267be7aac7aab1faab7987a7cbe44_l3.png)
We can apply the contraction mapping theorem on this interval to guarantee the existence of a unique fixed point
such that
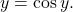
Then, for any

![Rendered by QuickLaTeX.com \cos x_0 \in [-1,1],](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-80a07b9ac4a16f69b4b803cb3562cc36_l3.png)
which guarantees the convergence of our sequence to the fixed point
We now briefly discuss the definition of continuity between metric spaces.
Definition
A map

between two metric spaces is
continuous if any of the following equivalent conditions hold:
- For any open
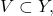
 is open.
is open.
- For every sequence
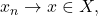
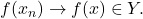
- For every
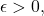 there exists a
there exists a 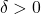 such that
such that  whenever
whenever 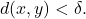
Similarly, one can define a local notion of continuity at a single point.
Definition:

is
continuous at 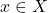
if:
- For all
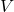 neighborhood of
neighborhood of  there exists a neighborhood
there exists a neighborhood 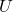 of
of 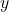 such that
such that 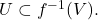
- For all
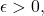 there exists a
there exists a 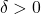 such that
such that  whenever
whenever 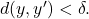
 implies
implies 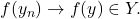
Examples:
- The function
 defined to be
defined to be 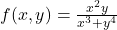 for
for  and
and  is not continuous at
is not continuous at  since setting
since setting  implies
implies 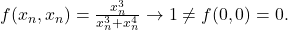
-
For a discrete metric space
 and a subset
and a subset  suppose
suppose 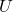 is equipped with the discrete metric
is equipped with the discrete metric  and
and  is equipped with an arbitrary metric
is equipped with an arbitrary metric 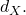 Then, the inclusion map
Then, the inclusion map  is always continuous, since
is always continuous, since  for
for  for
for 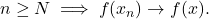
We now consider another very important property of sets in metric spaces known as connectedness.
Definition:
A set 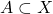 is said to be disconnected if there exist non-empty open sets
is said to be disconnected if there exist non-empty open sets  such that
such that  and
and 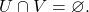 If a set is not disconnected, it is called connected.
If a set is not disconnected, it is called connected.
Definition:
A set 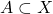 is called path-connected if for every
is called path-connected if for every  there exists a continuous map
there exists a continuous map ![Rendered by QuickLaTeX.com f:[0,1] \to X](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-175a7879aee359358f3125c6e6d78a81_l3.png) such that
such that  and
and  Such a map is called a path from
Such a map is called a path from 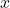 to
to 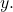
Examples:
- As seen in lecture, a set in
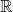 is connected if and only if it is an interval.
is connected if and only if it is an interval.
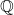 is not connected, since
is not connected, since  for some
for some  disconnects
disconnects 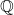 into two disjoint components.
into two disjoint components.
Proposition:
If  is continuous and
is continuous and 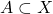 is connected, then
is connected, then 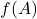 is connected in
is connected in 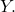
Proof:
Suppose not. Then, there exist  open such that
open such that  Then, by the topological definition of continuity,
Then, by the topological definition of continuity,  are open,
are open, 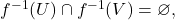 and
and  But this implies
But this implies  is disconnected, which is a contradiction.
is disconnected, which is a contradiction.
Proposition:
If a set  is path-connected, it is connected.
is path-connected, it is connected.
Proof:
For sake of contradiction, suppose  is path-connected but not connected. Then, there exist
is path-connected but not connected. Then, there exist 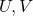 open such that
open such that  and
and 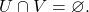 Pick
Pick 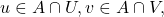 and a path
and a path ![Rendered by QuickLaTeX.com f: [0,1] \to A](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-30822d6b2bd20f2415d108b4a29abb2d_l3.png) such that
such that  Since the image of a connected set under a continuous map is connected,
Since the image of a connected set under a continuous map is connected, ![Rendered by QuickLaTeX.com f([0,1])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-d0fdf1d9a74dd8543add3c6b2f2e03eb_l3.png) is connected. But
is connected. But ![Rendered by QuickLaTeX.com f([0,1]) \subset U \cup V,](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-12bc0177a94709045c6819b1dbb6f2d7_l3.png)
 so
so ![Rendered by QuickLaTeX.com f([0,1])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-d0fdf1d9a74dd8543add3c6b2f2e03eb_l3.png) is disconnected, which is a contradiction.
is disconnected, which is a contradiction.
Corollary
![Rendered by QuickLaTeX.com C([0,1])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-c2d4a3a94234f090ffdf6f58e356b526_l3.png) is connected, since for any
is connected, since for any ![Rendered by QuickLaTeX.com f,g \in C([0,1]),](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-dbb1bcea1c408eb7cabcfc6e47a0ae4c_l3.png)
![Rendered by QuickLaTeX.com \gamma: [0,1] \to C([0,1])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-478eecd224b7caeae7ab7f7d15c924a4_l3.png) given by
given by  is a continuous map satisfying
is a continuous map satisfying 
![]()
![]()
![]()
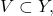
 is open.
is open.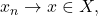
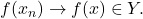
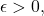 there exists a
there exists a 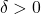 such that
such that  whenever
whenever 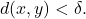
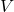 neighborhood of
neighborhood of  there exists a neighborhood
there exists a neighborhood 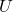 of
of 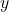 such that
such that 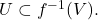
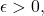 there exists a
there exists a 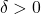 such that
such that  whenever
whenever 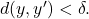
 implies
implies 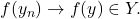
 defined to be
defined to be 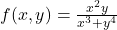 for
for  and
and  is not continuous at
is not continuous at  since setting
since setting  implies
implies 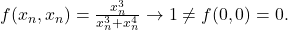
 and a subset
and a subset  suppose
suppose 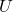 is equipped with the discrete metric
is equipped with the discrete metric  and
and  is equipped with an arbitrary metric
is equipped with an arbitrary metric 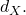 Then, the inclusion map
Then, the inclusion map  is always continuous, since
is always continuous, since  for
for  for
for 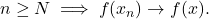
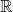 is connected if and only if it is an interval.
is connected if and only if it is an interval.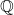 is not connected, since
is not connected, since  for some
for some  disconnects
disconnects  into two disjoint components.
into two disjoint components.