Skip to content
Easy
- Show that the image of a connected set under a continuous map is connected.
Solution:
Suppose not. Then, there exist  open such that
open such that  Then, by the topological definition of continuity,
Then, by the topological definition of continuity,  are open,
are open, 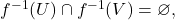 and
and  But this implies
But this implies  is disconnected, which is a contradiction.
is disconnected, which is a contradiction.
- Show that if a sequence
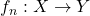 of continuous functions converges uniformly to a function
of continuous functions converges uniformly to a function 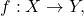 then
then  is continuous.
is continuous.
Solution:
Let  Then, there exists an
Then, there exists an 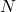 and a
and a 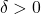 such that
such that 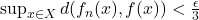 and
and 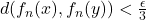 whenever
whenever 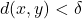 and
and  Then, by the triangle inequality,
Then, by the triangle inequality,
![Rendered by QuickLaTeX.com \[d(f(x),f(y)) \leq d(f(x),f_n(x)) + d(f_n(x),f_n(y)) + d(f_n(y),f(y)) < \frac{\epsilon}{3} + \frac{\epsilon}{3} + \frac{\epsilon}{3} = \epsilon\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-6de13ebb8958924da483c8fe330a6571_l3.png)
whenever 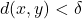 and
and 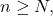 showing that
showing that  is continuous.
is continuous.
- Provide an example of a sequence of continuous functions
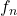 that converges pointwise to some function
that converges pointwise to some function 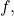 but does not converge uniformly to
but does not converge uniformly to 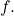
Solution:
Define ![Rendered by QuickLaTeX.com f_n:[0,1] \to \mathbb{R}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-dad2ee6674e819fe9cfb90924792dbc9_l3.png) given by
given by  Then,
Then,  for
for  and
and  so
so 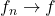 pointwise, where
pointwise, where  for
for  and
and 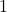 otherwise. But by the previous example, a uniformly convergent sequence of continuous functions converges to a continuous function, and since
otherwise. But by the previous example, a uniformly convergent sequence of continuous functions converges to a continuous function, and since  is not continuous,
is not continuous, 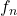 does not converge uniformly to
does not converge uniformly to 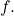
- Let
 be a function from a connected metric space
be a function from a connected metric space 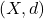 to a metric space
to a metric space 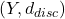 with the discrete metric. Show that
with the discrete metric. Show that  is continuous if and only if it is constant.
is continuous if and only if it is constant.
Solution:
Note that a constant function is trivially continuous, since 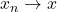 always implies
always implies 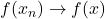 since
since 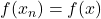 for all
for all 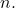 Conversely, using the sequential definition of continuity, suppose
Conversely, using the sequential definition of continuity, suppose  is continuous. Then, since the image of a connected set under a continuous map is connected,
is continuous. Then, since the image of a connected set under a continuous map is connected, 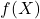 is connected. If
is connected. If 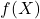 had at least two distinct elements
had at least two distinct elements 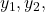 then
then 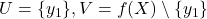 would be open sets (since every set in a discrete metric space is open) such that
would be open sets (since every set in a discrete metric space is open) such that 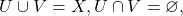 contradicting the fact that
contradicting the fact that 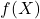 is connected. Thus,
is connected. Thus, 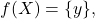 i.e.
i.e. 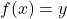 for all
for all 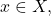 showing that
showing that  is constant. Consequently
is constant. Consequently  is continuous if and only if it is constant.
is continuous if and only if it is constant.
Medium
- Show that the topologist’s sine curve (the set defined in Problem 1 on HW3) is connected but not path-connected.
Solution:
Let  be the topologist’s sine curve. Note that
be the topologist’s sine curve. Note that 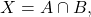 where
where 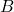 is an interval and is therefore path-connected. Moreover,
is an interval and is therefore path-connected. Moreover,  is path connected since the path
is path connected since the path ![Rendered by QuickLaTeX.com \gamma:[0,1] \to A](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-37044b83e8fa3827c4a12f8d2a7f7969_l3.png) such that
such that ![Rendered by QuickLaTeX.com \[\gamma(t) = \left(t x_1 + (1-t)x_2, \sin\left(\frac{1}{t x_2+(1-t)x_1}\right)\right)\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-da42e09ea9ab037d56e47d9ef0ec0f87_l3.png)
is such that ![Rendered by QuickLaTeX.com \[\gamma(0) = \left(x_1,\sin\left(\frac{1}{x_1}\right)\right),\gamma(1) = \left(x_2, \sin\left(\frac{1}{x_2}\right)\right).\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-32620c9aa400ba4b716722450fac730c_l3.png)
Thus, it suffices to show  and
and 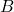 are connected but not path-connected.
Indeed,
are connected but not path-connected.
Indeed,  is not path-connected, since there is no path from the point
is not path-connected, since there is no path from the point 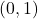 to the point
to the point 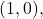 for if there were a continuous path
for if there were a continuous path ![Rendered by QuickLaTeX.com \gamma: [0,1] \to X](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-e41dce4d698574c99aefe18d523627f9_l3.png) with
with 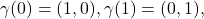 there would exist an
there would exist an 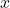 such that
such that ![Rendered by QuickLaTeX.com x_0 = \inf\{x \in [0,1]: \gamma(x) \in B\}.](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b3ca0b70554c5788fd136fbefcc901bc_l3.png) But then, there must exist a
But then, there must exist a  such that
such that 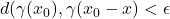 whenever
whenever 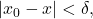 i.e.
i.e. 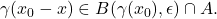 But note that
But note that 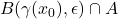 is disconnected, with each component being of the form
is disconnected, with each component being of the form 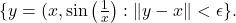 Thus, no such path exists, showing that
Thus, no such path exists, showing that  is not path-connected.
is not path-connected.
To show that  is connected, proceed by contradiction, and suppose
is connected, proceed by contradiction, and suppose 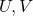 are open sets such that
are open sets such that 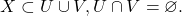 Without loss of generality, suppose
Without loss of generality, suppose 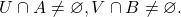 Let
Let 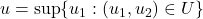 and
and 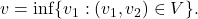 if
if  then for any
then for any 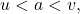 the point
the point 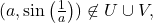 which is a contradiction. If
which is a contradiction. If 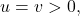 then
then 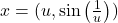 is either in
is either in 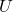 or in
or in 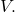 Without loss of generality, suppose
Without loss of generality, suppose  and note that since
and note that since 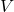 is open, there exist an open ball
is open, there exist an open ball 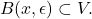 But this implies
But this implies 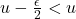 is an
is an 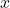 -coordinate of a point in
-coordinate of a point in  which contradicts the definition of
which contradicts the definition of 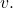 Finally, if
Finally, if 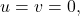 one notes that
one notes that 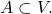 Since
Since 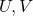 are open and
are open and  But
But 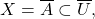 so
so 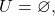 which is a contradiction. Thus, no such
which is a contradiction. Thus, no such  exist, showing that the topologist’s sine curve is connected.
exist, showing that the topologist’s sine curve is connected.
- Show that a continuous function on a compact metric space is uniformly continuous.
Solution:
Let  be a compact metric space and suppose
be a compact metric space and suppose  is continuous. Fix
is continuous. Fix  Since
Since  is continuous, for every
is continuous, for every 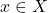 there exists a
there exists a  such that
such that 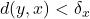 implies
implies 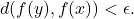 Note that
Note that  (we will justify the choice of radii later) is an open cover of
(we will justify the choice of radii later) is an open cover of 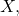 so by compactness, it has a finite subcover
so by compactness, it has a finite subcover 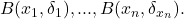 Then for
Then for 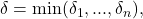 whenever
whenever 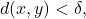
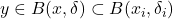 for some
for some 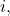 so
so 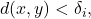 implying by the triangle inequality that
implying by the triangle inequality that ![Rendered by QuickLaTeX.com \[d(f(x),f(y)) \leq d(f(x),f(x_i)) + d(f(x_i),f(y))<\frac{\epsilon}{2}+\frac{\epsilon}{2} = \epsilon.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-575a4bd81ef3219e65c49751f00f565e_l3.png)
Since  is independent of
is independent of 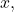 we conclude that
we conclude that  is uniformly continuous.
is uniformly continuous.
- Let
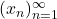 be a sequence of real numbers that converges to 0, and suppose
be a sequence of real numbers that converges to 0, and suppose 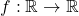 is uniformly continuous. Define a sequence
is uniformly continuous. Define a sequence 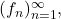 where
where 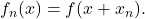 Show that
Show that 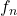 converges uniformly to
converges uniformly to 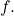
Solution:
Since  is uniformy continuous, for every
is uniformy continuous, for every 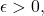 there exists
there exists 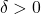 such that
such that 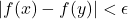 whenever
whenever 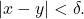 In particular, note that
In particular, note that 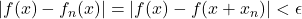 whenever
whenever  which is guaranteed for large enough
which is guaranteed for large enough 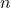 since
since 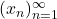 converges to 0. Since the choice of
converges to 0. Since the choice of  is independent of
is independent of 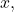 we thus conclude that
we thus conclude that 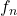 converges uniformly to
converges uniformly to 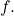
Challenging:
- Prove Dini’s theorem: let
 be a compact metric space, and let
be a compact metric space, and let 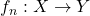 be a monotonically increasing sequence of functions, i.e.
be a monotonically increasing sequence of functions, i.e. 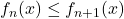 for all
for all 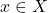 and
and 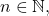 that converges pointwise to some function
that converges pointwise to some function 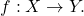 Furthermore, suppose
Furthermore, suppose  is continuous. Then,
is continuous. Then, 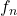 converges uniformly to
converges uniformly to 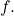
Solution:
Proceed by contradiction. Note that without loss of generality one can set 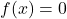 for all
for all  Then, since
Then, since 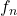 does not converge uniformly to 0, there exists an
does not converge uniformly to 0, there exists an 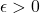 and a sequence
and a sequence 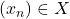 such that
such that 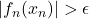 for all
for all 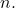 Since
Since  is compact,
is compact, 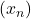 has a convergent subsequence
has a convergent subsequence 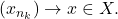 Then, since
Then, since 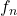 is continuous for all
is continuous for all 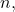 for any
for any 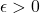 there exists a
there exists a 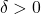 such that
such that
![Rendered by QuickLaTeX.com \[|f_{n_k}(x_{n_k}) - f_{n_k}(x)| < \frac{\epsilon}{2}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-eee4aad8cdfdc1c745f572db1feffe7c_l3.png)
whenever  This shows that
This shows that 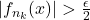 for
for 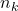 sufficiently large. But since
sufficiently large. But since 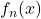 is an increasing sequence, it follows that
is an increasing sequence, it follows that ![Rendered by QuickLaTeX.com \[\lim_{n \to \infty} |f_n(x)| = \lim_{n_{k} \to \infty} |f_{n_k}(x)| = |f(x)|\geq \frac{\epsilon}{2},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-57bfd5c3963a9bbd4a550218b7bf4bf8_l3.png)
so 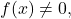 and we thus arrive at a contradiction. Consequently,
and we thus arrive at a contradiction. Consequently, 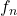 must converge uniformly to
must converge uniformly to 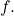
- Suppose
![Rendered by QuickLaTeX.com f_n: [a,b] \to \mathbb{R}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b0d968856bc0136031d7a26b0a67fd38_l3.png) is a sequence of Riemann integrable functions that converges uniformly to a function
is a sequence of Riemann integrable functions that converges uniformly to a function ![Rendered by QuickLaTeX.com f:[a,b] \to \mathbb{R}.](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-8052f31777c8caed3926793dea952bc0_l3.png) Show that
Show that  is Riemann integrable and
is Riemann integrable and ![Rendered by QuickLaTeX.com \[\int_a^b f_n(x)dx \to \int_a^b f(x)dx.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-583ddd9377e729e0658f9c9b097df047_l3.png)
Solution:
By the equivalent conditions for Riemann integrability, it suffices to show that there exists a sequence of partitions 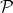 such that
such that
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f(x) - \inf_{[x_i,x_{i+1}]} f(x)) (x_{i+1}-x_i) \to 0.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b8f9ff12c16d00af713dcf09f8eb8dae_l3.png)
But note that by the triangle inequality, ![Rendered by QuickLaTeX.com \[|\sup f(x) - \inf f(x)| \leq |\sup f(x) - \sup f_n(x)| + |\sup f_n(x)-\inf f_n(x)| + |\inf f_n(x)-\inf f(x)|,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f48beda2e3a5e0d35042f3cd3c00fe02_l3.png)
where one can pick a sequence of equally spaced 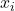 with
with 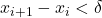 (for example,
(for example, 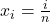 for
for 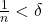 ) such that
) such that 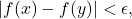 i.e.
i.e. ![Rendered by QuickLaTeX.com |\sup_{[x_i,x_{i+1}]} f(x) - \inf_{[x_i,x_{i+1}]} f(x)| <\epsilon](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9c16ade0c77ffd9384048ec981e368ba_l3.png) for
for ![Rendered by QuickLaTeX.com x,y \in [x_i,x_{i+1}]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-c693d7cf22f50e3fd8da551729d138a2_l3.png) (since
(since 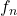 are continuous on a compact set, i.e. uniformly continuous). Picking
are continuous on a compact set, i.e. uniformly continuous). Picking 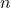 large enough such that
large enough such that 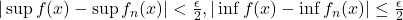 and summing over all intervals yields
and summing over all intervals yields
![Rendered by QuickLaTeX.com \[|\sup f(x) - \inf f(x)| \leq \epsilon + \sup f_n(x) -\inf f_n(x),\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-d60688bd3366543eeb00c9ec68f142e9_l3.png)
so summing over all intervals yields
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f(x) & - \inf_{[x_i,x_{i+1}]} f(x)) (x_{i+1}-x_i) \\ & \leq \sum_{i=0}^{n-1} \epsilon (x_{i+1}-x_i) + \sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f_n(x) - \inf_{[x_i,x_{i+1}]} f_n(x)) (x_{i+1}-x_i)\\ & = \epsilon (b-a)+ \sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f_n(x) - \inf_{[x_i,x_{i+1}]} f_n(x)) (x_{i+1}-x_i). \end{split} \end{equation*}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-05efc2e3c79a5d89f75aacf2d1871c53_l3.png)
We now note that since 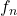 is Riemann integrable, there exists a sequence of partitions such that for any
is Riemann integrable, there exists a sequence of partitions such that for any 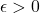
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f_n(x) - \inf_{[x_i,x_{i+1}]} f_n(x)) (x_{i+1}-x_i)< \epsilon.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-86719c5f9974187a5b64c8b7d593317f_l3.png)
Taking a common refinement of this sequence with our partition, we get that ![Rendered by QuickLaTeX.com \[\sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f(x) - \inf_{[x_i,x_{i+1}]} f(x)) (x_{i+1}-x_i) < \epsilon (b-a+1),\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-0ba0871a3b8248bcc745436586948313_l3.png)
which demonstrates that there exists a sequence of partitions that satisfies the condition for Riemann integrability. Thus,  is Riemann integrable. Finally,
by uniform convergence, for sufficiently large
is Riemann integrable. Finally,
by uniform convergence, for sufficiently large 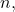
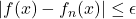 implies
implies ![Rendered by QuickLaTeX.com \[f_n(x) - \epsilon \leq f(x) \leq f_n(x) + \epsilon,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-49232c890b1018ee27fd18252ff64237_l3.png)
and integrating each side on ![Rendered by QuickLaTeX.com [a,b]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png) yields
yields
![Rendered by QuickLaTeX.com \[\int_a^b f_n(x) dx - \epsilon (b-a) \leq \int_a^b f(x) dx \leq \int_a^b f_n(x) dx + \epsilon (b-a),\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-10236bfedbed9ede55f31b0c8b2db209_l3.png)
so ![Rendered by QuickLaTeX.com \[\left|\int_a^b f_n(x) dx -\int_a^b f(x) dx\right|\leq\epsilon(b-a).\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-0d7b87002aeed086b33646d4cbd120a4_l3.png)
Letting 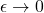 shows that
shows that ![Rendered by QuickLaTeX.com \[\int_a^b f_n(x) dx \to \int_a^b f(x) dx,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b9b1912605d10690eb232f572bdaa0c4_l3.png)
which completes the proof.
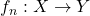 of continuous functions converges uniformly to a function
of continuous functions converges uniformly to a function 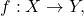 then
then  is continuous.
is continuous.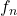 that converges pointwise to some function
that converges pointwise to some function 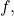 but does not converge uniformly to
but does not converge uniformly to 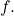
 be a function from a connected metric space
be a function from a connected metric space 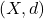 to a metric space
to a metric space 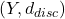 with the discrete metric. Show that
with the discrete metric. Show that  is continuous if and only if it is constant.
is continuous if and only if it is constant.![]()
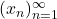 be a sequence of real numbers that converges to 0, and suppose
be a sequence of real numbers that converges to 0, and suppose 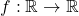 is uniformly continuous. Define a sequence
is uniformly continuous. Define a sequence 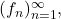 where
where 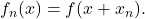 Show that
Show that 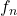 converges uniformly to
converges uniformly to 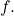
![]()
![]()
![]()
 be a compact metric space, and let
be a compact metric space, and let 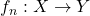 be a monotonically increasing sequence of functions, i.e.
be a monotonically increasing sequence of functions, i.e. 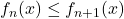 for all
for all 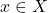 and
and 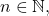 that converges pointwise to some function
that converges pointwise to some function 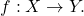 Furthermore, suppose
Furthermore, suppose  is continuous. Then,
is continuous. Then, 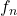 converges uniformly to
converges uniformly to 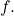
![Rendered by QuickLaTeX.com f_n: [a,b] \to \mathbb{R}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b0d968856bc0136031d7a26b0a67fd38_l3.png) is a sequence of Riemann integrable functions that converges uniformly to a function
is a sequence of Riemann integrable functions that converges uniformly to a function ![Rendered by QuickLaTeX.com f:[a,b] \to \mathbb{R}.](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-8052f31777c8caed3926793dea952bc0_l3.png) Show that
Show that  is Riemann integrable and
is Riemann integrable and ![Rendered by QuickLaTeX.com \[\int_a^b f_n(x)dx \to \int_a^b f(x)dx.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-583ddd9377e729e0658f9c9b097df047_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f(x) - \inf_{[x_i,x_{i+1}]} f(x)) (x_{i+1}-x_i) \to 0.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b8f9ff12c16d00af713dcf09f8eb8dae_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f(x) & - \inf_{[x_i,x_{i+1}]} f(x)) (x_{i+1}-x_i) \\ & \leq \sum_{i=0}^{n-1} \epsilon (x_{i+1}-x_i) + \sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f_n(x) - \inf_{[x_i,x_{i+1}]} f_n(x)) (x_{i+1}-x_i)\\ & = \epsilon (b-a)+ \sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f_n(x) - \inf_{[x_i,x_{i+1}]} f_n(x)) (x_{i+1}-x_i). \end{split} \end{equation*}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-05efc2e3c79a5d89f75aacf2d1871c53_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f_n(x) - \inf_{[x_i,x_{i+1}]} f_n(x)) (x_{i+1}-x_i)< \epsilon.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-86719c5f9974187a5b64c8b7d593317f_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{n-1} (\sup_{[x_i,x_{i+1}]} f(x) - \inf_{[x_i,x_{i+1}]} f(x)) (x_{i+1}-x_i) < \epsilon (b-a+1),\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-0ba0871a3b8248bcc745436586948313_l3.png)
![]()
![]()
![]()
![]()