Week 4, Stepan Malkov

We begin by finishing up a proof that we didn’t get to cover last time.

Theorem (Heine-Borel Theorem):

A set is compact in $\mathbb{R}^n$ if and only if it is closed and bounded.

Proof:

We prove the statement by induction. For $n=1,$ a closed and bounded set is sequentially compact by Bolzano-Weierstrass, so it is compact. Now, suppose the statement is true for $n-1.$ Suppose $A$ is a closed and bounded subset of $\mathbb{R}^n$ consisting of the points $\{(b, a): b \in \mathbb{R}^{n-1}, a \in \mathbb{R}\}$ and let

$A_n = \{a \in \mathbb{R}: (b,a) \in A\}.$

Let $(u_k)_{k=1}^\infty, u_k = (b_k, a_k) \in A$ be a sequence. Then, by Bolzano-Weierstrass, there exists a convergent subsequence $a_{k_i} \to a \in \mathbb{R}, a_k \in A_n.$ By our inductive hypothesis, $(b_{k_i})$ has a convergent subsequence $c_j \to c \in \mathbb{R}^{n-1}$ . Then,

$(c_j,a_j) \to (c,a) \in A,$

is a subsequence of $(u_k)$ that converges in $A,$ and we are finished.

Remark: It is not generally true that a closed and bounded set is compact. As an example, take $(X,d)$ to be a metric space, where $X$ is infinite.

Practice Problems for Midterm 1:

Let 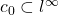$c_0 \subset l^\infty$ be the set of sequences that converge to 0, equipped with the 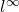$l^ \infty$ metric. Is 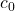$c_0$ complete? Is 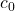$c_0$ compact?
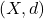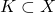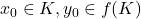Suppose $(X,d)$ is a metric space, $K \subset X$ is a compact set, and $f: X \to X$ is a continuous map. Show that there exist $x_0 \in K, y_0 \in f(K)$ such that
$d(x_0,y_0) = \inf_{x \in K, y \in f(K)} d(x,y).$
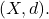Let $K_1 \supset K_2 \supset ...$ be a sequence of nonempty compact subsets of a metric space $(X,d).$ Show that 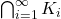$\bigcap_{i=1}^\infty K_i$ is nonempty.