Skip to content
Easy:
- Show that a sequence
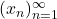 has a convergent subsequence if and only if the set
has a convergent subsequence if and only if the set  has an adherent point.
has an adherent point.
Solution:
Suppose  is an adherent point of
is an adherent point of  Then, for every
Then, for every 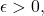 there exists an
there exists an 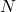 such that
such that 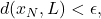 meaning one can construct a subsequence
meaning one can construct a subsequence  with
with  such that
such that 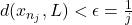 (as otherwise, there would exist an
(as otherwise, there would exist an 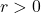 such that
such that  for all
for all 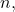 contradicting the fact that
contradicting the fact that 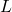 is an adherent point. By definition of a convergent subsequence, this implies
is an adherent point. By definition of a convergent subsequence, this implies  i.e.
i.e. 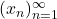 has a convergent subsequence. Conversely, if
has a convergent subsequence. Conversely, if  is a convergent subsequence converging to
is a convergent subsequence converging to 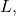 note that for any
note that for any 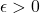 and
and 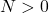 there exists an
there exists an  such that
such that  implying that
implying that 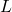 is an adherent point of the sequence
is an adherent point of the sequence 
- Show that a closed subset
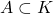 of a compact metric space
of a compact metric space  in is compact.
in is compact.
Solution: Let 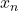 be a sequence in
be a sequence in 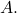 Then, it has a convergent subsequence
Then, it has a convergent subsequence  in
in 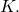 But since
But since  is closed,
is closed, 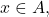 so every sequence is
so every sequence is  has a convergent subsequence in
has a convergent subsequence in 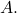 Thus,
Thus,  is sequentially compact, i.e. it is compact.
is sequentially compact, i.e. it is compact.
- Let
 be a sequence of compact subsets of a metric space. Show
be a sequence of compact subsets of a metric space. Show  is non-empty.
is non-empty.
Solution:
Form a sequence 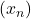 such that
such that 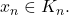 Then, this sequence has a convergent subsequence
Then, this sequence has a convergent subsequence  Since
Since  for
for  and
and 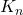 is compact and therefore closed, it follows that
is compact and therefore closed, it follows that  for all
for all 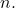 Thus,
Thus,  i.e. the intersection is nonempty.
i.e. the intersection is nonempty.
- Show that every Cauchy sequence is bounded.
Solution:
Let  Then, by the definition of a Cauchy sequence, for some
Then, by the definition of a Cauchy sequence, for some 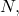
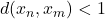 for
for 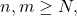 so
so  contains all elements of the sequence, i.e. the sequence is bounded.
contains all elements of the sequence, i.e. the sequence is bounded.
Medium:
- Consider
![Rendered by QuickLaTeX.com C([0,1])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-c2d4a3a94234f090ffdf6f58e356b526_l3.png) with the metric of uniform convergence. Let
with the metric of uniform convergence. Let ![Rendered by QuickLaTeX.com (f_n)_{n=1}^\infty \subset C([0,1])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-12a0a65c3f9fdc27ffff322b83e59e18_l3.png) be a sequence defined by
be a sequence defined by  Show that the set
Show that the set  is not compact in
is not compact in ![Rendered by QuickLaTeX.com C([0,1]).](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cd0f85de59a52990c44cea06501c57bf_l3.png)
Solution:
Note that since  pointwise, any convergent sequence of distinct elements would have a further convergent subsequence
pointwise, any convergent sequence of distinct elements would have a further convergent subsequence 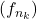 that converges to
that converges to 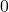 in
in ![Rendered by QuickLaTeX.com C([0,1]).](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cd0f85de59a52990c44cea06501c57bf_l3.png) But
But 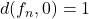 for all
for all 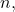 so there any such sequence has no convergent subsequence, i.e. it is not compact in
so there any such sequence has no convergent subsequence, i.e. it is not compact in ![Rendered by QuickLaTeX.com C([a,b]).](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-48d3b3b6d1b2d67cc2d225caa01454b5_l3.png)
- A metric space
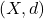 is called totally bounded if for every
is called totally bounded if for every 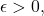 there exist finitely many points
there exist finitely many points  such that
such that  Show that a metric space is compact if and only if it is complete and totally bounded.
Show that a metric space is compact if and only if it is complete and totally bounded.
Solution:
Suppose  is compact. Then, let
is compact. Then, let 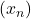 be a Cauchy sequence, and
be a Cauchy sequence, and  be a convergent subsequence. Since
be a convergent subsequence. Since ![Rendered by QuickLaTeX.com \[d(x_n,x) \leq d(x_n,x_{n_k}) + d(x_{n_k},x) < \frac{\epsilon}{2}+\frac{\epsilon}{2} = \epsilon\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5caa4eda68bb466dd53247fc55af8f0d_l3.png)
for sufficiently large 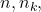 one gets that
one gets that 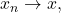 i.e. a Cauchy sequence converges. Thus
i.e. a Cauchy sequence converges. Thus  is complete.
is complete.
Now, for any 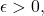 let
let  be an open cover of
be an open cover of 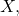 which by compactness must have a finite subcover
which by compactness must have a finite subcover  Thus, there exist finitely many balls that cover
Thus, there exist finitely many balls that cover 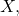 i.e.
i.e.  is totally bounded.
is totally bounded.
Conversely, suppose  is complete and totally bounded, and let
is complete and totally bounded, and let 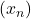 be a sequence. Cover
be a sequence. Cover  by balls of radius
by balls of radius 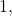 and note that at least one of the balls
and note that at least one of the balls  must have infinitely many elements of
must have infinitely many elements of 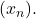 Pick one such element
Pick one such element  and cover
and cover  by balls of radius
by balls of radius 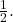 Note that there must exist a ball
Note that there must exist a ball  such that
such that  has infinitely many elements of
has infinitely many elements of 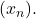 Pick one such element
Pick one such element  and proceed in this fashion by covering
and proceed in this fashion by covering  with balls of radius
with balls of radius  to construct a subsequence
to construct a subsequence  By construction,
By construction,  for
for  so
so  for
for  i.e. the sequence is Cauchy. By completeness, it converges to some
i.e. the sequence is Cauchy. By completeness, it converges to some  Thus, any sequence
Thus, any sequence 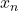 has a convergent subsequence
has a convergent subsequence  showing that
showing that  is compact. This shows that
is compact. This shows that  is compact if and only if it is complete and totally bounded.
is compact if and only if it is complete and totally bounded.
- Show
 is complete.
is complete.
Solution:
Let  be a Cauchy sequence. Then,
be a Cauchy sequence. Then, 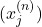 is a Cauchy sequence in
is a Cauchy sequence in 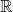 for each fixed
for each fixed 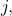 and thus converges to some
and thus converges to some 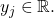 I claim that
I claim that  Indeed, if one picks an
Indeed, if one picks an 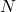 such that
such that  for
for 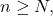 taking the limit in
taking the limit in 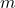 shows that
shows that
![Rendered by QuickLaTeX.com \[\lim_{m \to \infty} |x_j^{(n)}-x_j^{(m)}| = |x_j^{(n)}-y_j| \leq \frac{\epsilon}{2},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-2f7c623b9f24976b0d1257e3f5b770e4_l3.png)
so
![Rendered by QuickLaTeX.com \[d(x^{(n)},y) = \sup_{j} |x_j^{(n)}-y_j| \leq \frac{\epsilon}{2} < \epsilon,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9dc6075426c0fc08b0e2c55e397e706e_l3.png)
i.e.  in
in 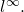 Thus, a Cauchy sequence in
Thus, a Cauchy sequence in  converges, showing that
converges, showing that  is complete.
is complete.
Challenging
- Let
![Rendered by QuickLaTeX.com \mathcal{B} = \{f \in C([0,1]): |f(x)|\leq 1, x \in [0,1]\}.](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-58494598d34af07ba4253c9d87fbefd1_l3.png) Determine whether
Determine whether 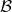 is complete, bounded, totally bounded, and compact.
is complete, bounded, totally bounded, and compact.
Solution:
Note that  so it is bounded. It is complete since if
so it is bounded. It is complete since if ![Rendered by QuickLaTeX.com \sup_{x \in [0,1]} |f_n(x)-f_m(x)| < \epsilon](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-923eab0ab279d473a35abb126e000908_l3.png) for
for 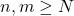 for some
for some 
 is a Cauchy sequence for each
is a Cauchy sequence for each 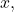 so it converges to some
so it converges to some  Now, by the same argument as in the proof of Problem 7,
Now, by the same argument as in the proof of Problem 7,
![Rendered by QuickLaTeX.com \[\lim_{m \to \infty} |f_n(x) - f_m(x)| \leq \frac{\epsilon}{2}<\epsilon\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cc2bd255cb55c15a59291bdf65030505_l3.png)
for 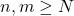 such that
such that  so
so ![Rendered by QuickLaTeX.com \[\sup_{x \in [0,1]} |f_n(x)-f(x)| \leq \frac{\epsilon}{2} < \epsilon,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-757f5670d06c55dceee1f2f6e15ea181_l3.png)
i.e. 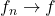 in
in ![Rendered by QuickLaTeX.com C([0,1]).](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cd0f85de59a52990c44cea06501c57bf_l3.png) We now claim that
We now claim that 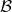 is not compact. Let
is not compact. Let  Then, by Problem 5, this sequence has no convergent subsequence in
Then, by Problem 5, this sequence has no convergent subsequence in ![Rendered by QuickLaTeX.com C([0,1]),](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-301bbbc5d50c4afac90579b3cf041de0_l3.png) so it has no convergent subsequence in
so it has no convergent subsequence in  showing that
showing that 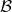 is not compact. Finally, since
is not compact. Finally, since 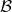 is complete but not compact, and a set is compact if and only if it is complete and totally bounded, we conclude that
is complete but not compact, and a set is compact if and only if it is complete and totally bounded, we conclude that 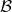 is not totally bounded.
is not totally bounded.
- The following outlines the proof of an important theorem known as the Contraction Mapping Principle. The Contraction Mapping Principle states that if
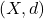 is a complete metric space and
is a complete metric space and  is a contraction on
is a contraction on 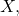 that is,
that is, 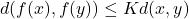 for some
for some  then the map
then the map  has a unique fixed point, i.e. a point
has a unique fixed point, i.e. a point 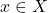 such that
such that 
- Pick a point
 and define
and define  Show that
Show that 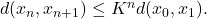
Solution: Iterating the contraction equation 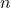 times yields
times yields ![Rendered by QuickLaTeX.com \[d(x_n,x_{n+1}) \leq K d(x_{n-1},x_n) \leq ... \leq K^n d(x_0,x_1).\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9e226567ad8d61b9e2e6ddad7dd737c3_l3.png)
- Use part i), the triangle inequality, and the geometric series formula to show that
 Conclude that
Conclude that 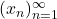 is Cauchy, and therefore converges to some
is Cauchy, and therefore converges to some 
Solution:
By the triangle inequality and the geometric series formula, one obtains ![Rendered by QuickLaTeX.com \[d(x_n,x_m) \leq (K^n + K^{n+1}+... + K^{m-1}) d(x_0,x_1) = K^n(1 + K + ... +K^{m-1}) d(x_0,x_1) \leq \frac{K^n}{1-K} d(x_0,x_1) \to 0\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-94e48c6758bae82da3dbc9e5ddf8bf81_l3.png)
as 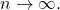 Thus, the sequence is Cauchy, so it has a limit
Thus, the sequence is Cauchy, so it has a limit 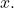
- Show that
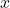 is a fixed point of
is a fixed point of 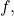 and use proof by contradiction to show that the fixed point must be unique.
and use proof by contradiction to show that the fixed point must be unique.
Solution: ![Rendered by QuickLaTeX.com \[f(x) = f(\lim_{n \to \infty} x_n) = \lim_{n \to \infty} f(x_n) = \lim_{n \to \infty} x_{n+1} = x,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-279788f0ebaa51c0206cdac2ddc267c4_l3.png)
so 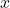 is a fixed point of
is a fixed point of 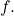 If there were two fixed points
If there were two fixed points 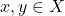 then
then 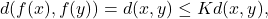 which is a contradicton, so uniqueness follows.
which is a contradicton, so uniqueness follows.
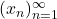 has a convergent subsequence if and only if the set
has a convergent subsequence if and only if the set  has an adherent point.
Solution:
Suppose
has an adherent point.
Solution:
Suppose 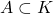 of a compact metric space
of a compact metric space  in is compact.
Solution: Let
in is compact.
Solution: Let  be a sequence of compact subsets of a metric space. Show
be a sequence of compact subsets of a metric space. Show  is non-empty.
Solution:
Form a sequence
is non-empty.
Solution:
Form a sequence ![Rendered by QuickLaTeX.com C([0,1])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-c2d4a3a94234f090ffdf6f58e356b526_l3.png) with the metric of uniform convergence. Let
with the metric of uniform convergence. Let ![Rendered by QuickLaTeX.com (f_n)_{n=1}^\infty \subset C([0,1])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-12a0a65c3f9fdc27ffff322b83e59e18_l3.png) be a sequence defined by
be a sequence defined by  Show that the set
Show that the set  is not compact in
is not compact in ![Rendered by QuickLaTeX.com C([0,1]).](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cd0f85de59a52990c44cea06501c57bf_l3.png) Solution:
Note that since
Solution:
Note that since 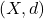 is called totally bounded if for every
is called totally bounded if for every 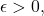 there exist finitely many points
there exist finitely many points  such that
such that  Show that a metric space is compact if and only if it is complete and totally bounded.
Solution:
Suppose
Show that a metric space is compact if and only if it is complete and totally bounded.
Solution:
Suppose  is complete.
Solution:
Let
is complete.
Solution:
Let ![]()
![]()
![]()
![Rendered by QuickLaTeX.com \mathcal{B} = \{f \in C([0,1]): |f(x)|\leq 1, x \in [0,1]\}.](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-58494598d34af07ba4253c9d87fbefd1_l3.png) Determine whether
Determine whether 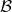 is complete, bounded, totally bounded, and compact.
Solution:
Note that
is complete, bounded, totally bounded, and compact.
Solution:
Note that 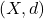 is a complete metric space and
is a complete metric space and  is a contraction on
is a contraction on 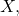 that is,
that is, 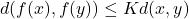 for some
for some  then the map
then the map  has a unique fixed point, i.e. a point
has a unique fixed point, i.e. a point 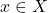 such that
such that 
 and define
and define  Show that
Show that 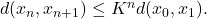 Solution: Iterating the contraction equation
Solution: Iterating the contraction equation  Conclude that
Conclude that 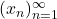 is Cauchy, and therefore converges to some
is Cauchy, and therefore converges to some  Solution:
By the triangle inequality and the geometric series formula, one obtains
Solution:
By the triangle inequality and the geometric series formula, one obtains 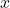 is a fixed point of
is a fixed point of 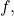 and use proof by contradiction to show that the fixed point must be unique.
Solution:
and use proof by contradiction to show that the fixed point must be unique.
Solution: 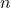 times yields
times yields ![Rendered by QuickLaTeX.com \[d(x_n,x_{n+1}) \leq K d(x_{n-1},x_n) \leq ... \leq K^n d(x_0,x_1).\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9e226567ad8d61b9e2e6ddad7dd737c3_l3.png)
![Rendered by QuickLaTeX.com \[d(x_n,x_m) \leq (K^n + K^{n+1}+... + K^{m-1}) d(x_0,x_1) = K^n(1 + K + ... +K^{m-1}) d(x_0,x_1) \leq \frac{K^n}{1-K} d(x_0,x_1) \to 0\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-94e48c6758bae82da3dbc9e5ddf8bf81_l3.png)
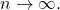 Thus, the sequence is Cauchy, so it has a limit
Thus, the sequence is Cauchy, so it has a limit 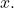
![Rendered by QuickLaTeX.com \[f(x) = f(\lim_{n \to \infty} x_n) = \lim_{n \to \infty} f(x_n) = \lim_{n \to \infty} x_{n+1} = x,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-279788f0ebaa51c0206cdac2ddc267c4_l3.png)
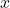 is a fixed point of
is a fixed point of 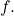 If there were two fixed points
If there were two fixed points 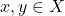 then
then 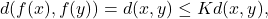 which is a contradicton, so uniqueness follows.
which is a contradicton, so uniqueness follows.
![]()
![]()