Week 10: Introduction to Analysis in Several Variables

In our last week, we introduce the basics of multivariable analysis.

Definition:

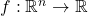
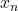
A partial derivative of $f: \mathbb{R}^n \to \mathbb{R}$ with respect to the variable $x_n$ is the limit

$f_{x_m}(a_1,a_2,...,a_n) = \lim_{h \to 0} \frac{f(a_1,...,a_m+h,...,a_n)-f(a_1,...,a_n)}{h},$

if the limit exists.

Example:

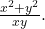
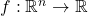
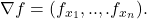
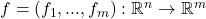
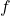
The function $\frac{x^2+y^2}{xy}.$ Recall that for a multivariable function $f: \mathbb{R}^n \to \mathbb{R}$ one defines the gradient $\nabla f = (f_{x_1},..,.f_{x_n}).$ In similar fashion, for a multivariable function $f=(f_1,...,f_m):\mathbb{R}^n \to \mathbb{R}^m$ with multiple outputs, define the (total) derivative of $f$ to be

$Df(x) = \begin{bmatrix} \nabla f_1 \\ \nabla f_2 \\ ... \\ \nabla f_m \\ \end{bmatrix}=\begin{bmatrix} (f_1)_{x_1}(x) & (f_1)_{x_2}(x) & ... & (f_1)_{x_n}(x) \\ (f_2)_{x_1}(x) & ... & ... & (f_2)_{x_n}(x) \\ ... & ... & ... & ... \\ (f_m)_{x_1}(x) & (f_m)_{x_2}(x) & ... & (f_m)_{x_n}(x) \\ \end{bmatrix}$

Definition:

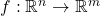
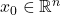
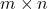
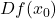
$f: \mathbb{R}^n \to \mathbb{R}^m$ is differentiable at $x_0 \in \mathbb{R}^n$ if there exists an $m \times n$ matrix $Df(x_0)$ such that

$f(x_0+h)=f(x) + Df(x_0) h+r(h),$

where

$\lim_{\|h\|\to 0} \frac{r(h)}{\|h\|}=0.$