Easy
- Let
![Rendered by QuickLaTeX.com X=C([a,b])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-e68c5cff77e78d001bd4fe3e774d4601_l3.png) be the space of continuous functions on the interval
be the space of continuous functions on the interval ![Rendered by QuickLaTeX.com [a,b].](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-680fa8adf874c40654e0874dc3509d0f_l3.png) Show that the map
Show that the map  defined by
defined by
is a metric, thus making![Rendered by QuickLaTeX.com \[d(f,g) = \max_{x \in [0,1]}[f(x)-g(x)]\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-68cc9c04796eb87052a2920728d766e1_l3.png)
 into a metric space.
into a metric space. - Let
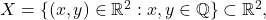 considered as a metric subspace. Find the boundary of
considered as a metric subspace. Find the boundary of  in
in 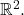
-
Let
 be a metric space. Suppose
be a metric space. Suppose  and
and 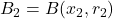 are open balls in
are open balls in  . Prove the following statement or find a counterexample: if the union
. Prove the following statement or find a counterexample: if the union  is an open ball, then either
is an open ball, then either 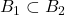 or
or 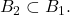
- Let
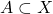 be a subset of a metric space. Show that
be a subset of a metric space. Show that 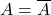 if and only if for every sequence
if and only if for every sequence 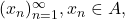 if
if  then
then 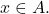
Solution:
Note that ![]()
![]()
![]()
Solution:
SinceSolution:
PickSolution:
SupposeIntermediate
- Let
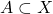 be a subset of a metric space. Show that
be a subset of a metric space. Show that  is closed in
is closed in  if and only if for every open ball
if and only if for every open ball  contained in
contained in 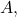
 is contained in
is contained in 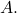
- Let
![Rendered by QuickLaTeX.com Y = \mathcal{P}([0,1])](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-47e6fc0f709f0985c2f366e8bcc7c38a_l3.png) be the power set of
be the power set of ![Rendered by QuickLaTeX.com [0,1],](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-6db8faf1e9c67c389a413693a0e1cc18_l3.png) that is, the set of subsets of
that is, the set of subsets of ![Rendered by QuickLaTeX.com [0,1].](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-fe398ab3182eef80acc301bd41f995f8_l3.png) Let
Let ![Rendered by QuickLaTeX.com A,B \subset [0,1],](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-f4a1113dad348deb6e072fa2bc97db4d_l3.png) and define
and define  by
by  Is
Is 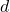 a metric?
a metric? - If
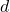 is a metric,
is a metric, 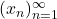 is a sequence, and
is a sequence, and  converges, is it true that
converges, is it true that 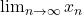 exists?
exists?
Note:
The problem as originally stated was not correct. As a counter example, takeSolution:
No, since for any ![]()
Solution:
No. As an example, takeChallenging
-
A set that is as a countable intersection of open sets is called a
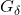 set, and a set that is a countable union of closed sets is called an
set, and a set that is a countable union of closed sets is called an  set. Show that the irrationals are a
set. Show that the irrationals are a 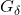 set.
set.
- Since the rationals can be written as a countable union of closed sets
 by de Morgan’s laws, the irrationals can be written as a countable intersection of open sets
by de Morgan’s laws, the irrationals can be written as a countable intersection of open sets
which is a![Rendered by QuickLaTeX.com \[\mathbb{Q}^c = \left(\bigcup_{q \in \mathbb{Q}} \{q\}\right)^c = \bigcap_{q \in \mathbb{Q}} \{q\}^c = \bigcap_{q \in \mathbb{Q}} \mathbb{R} \setminus \{q\},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ad79290a407057ffc4ca5f84d1cf9a09_l3.png)
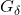 set since the complement of a closed set is an open set.
set since the complement of a closed set is an open set.
- A metric space
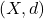 is called an ultrametric space if the condition
is called an ultrametric space if the condition
is replaced by the stronger condition![Rendered by QuickLaTeX.com \[d(x,z) \leq d(x,y) + d(y,z)\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-6eab0a799b033934f9be76c3f576f3a8_l3.png)
for all![Rendered by QuickLaTeX.com \[d(x,z) \leq \max(d(x,y),d(x,z))\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-e0a32aa51bf246287fde0637cd165874_l3.png)
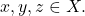
- Give an example of an ultrametric space.
- Show that every open ball is closed in
 and every closed ball is open in
and every closed ball is open in 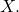
- An example of an ultrametric space is any set
 with the discrete metric, which is easily verified to be a metric. It is an ultrametric since if
with the discrete metric, which is easily verified to be a metric. It is an ultrametric since if 
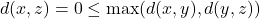 for any
for any  and if
and if  then either
then either  or
or  i.e.
i.e.
Thus,![Rendered by QuickLaTeX.com \[d(x,z) = 1 \leq \max(d(x,y),d(x,z)).\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9c5fc4ddf8afe05ad3da8d1827baf8d4_l3.png)
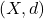 is indeed an ultrametric space.
is indeed an ultrametric space. - Let
 be an open ball in
be an open ball in  and let
and let  be a sequence such that
be a sequence such that  Then,
Then,
(since![Rendered by QuickLaTeX.com \[d(x,y) \leq \max(d(x,y_n),d(y_n,y)) = d(x,y_n) < r,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-32bfb6e27239d15095acce903bc318aa_l3.png)
 as
as 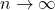 ), so
), so 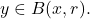 Thus,
Thus,  is closed. Similarly, let
is closed. Similarly, let 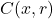 be a closed ball in
be a closed ball in  and let
and let  Then, for
Then, for  such that
such that 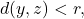
i.e.![Rendered by QuickLaTeX.com \[d(x,z) \leq \max(d(x,y),d(y,z)) < r,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-05a343eb417101c9278fee3558609ba7_l3.png)
 Thus,
Thus, 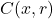 is open.
is open.