Week 1, Stepan Malkov

$\[\]$

The Riemann Integral

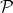
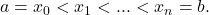
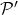
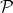
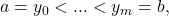
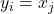
Take an interval $[a,b].$ Define a partition $\mathcal{P}$ to be a set $a=x_0<x_1<...<x_n=b.$ Define a refinement $\mathcal{P}'$ of a partition $\mathcal{P}$ to be a set $a=y_0<...<y_m=b,$ where $y_i = x_j$ for all $i.$

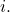
Proposition:

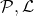
Any two partitions $\mathcal{P},\mathcal{L}$ have a common refinement.

Proof:

Take $\mathcal{P} \cup \mathcal{L}.$

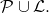
For $f:[a,b] \to \mathbb{C},$ we define the lower and upper sums

$L(f,\mathcal{P}) = \sum_{i=0}^{n-1} \inf_{x \in [x_i,x_{i+1}]} [f(x)](x_{i+1}-x_i)$

and

$U(f,\mathcal{P}) = \sum_{i=0}^{n-1} \sup_{x \in [x_i, x_{i+1}]} [f(x)](x_{i+1}-x_i).$

Proposition:

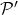
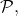
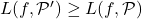
If $\mathcal{P}'$ is a refinement of $\mathcal{P},$ then $L(f,\mathcal{P'}) \geq L(f,\mathcal{P})$ and $U(f,\mathcal{P'}) \leq U(f,\mathcal{P}).$

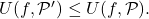
Proof:

Follows immediately from the fact that if $[y_j,y_{j+1}] \subseteq [x_i,x_{i+1}],$ then $\inf_{[y_j,y_{j+1}]} f(x) \geq \inf_{[x_i,x_{i+1}]} f(x)$ and $\sup_{[y_j,y_{j+1}]} f(x) \leq \sup_{[x_i,x_{i+1}]} f(x).$

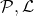
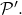
Take partitions $\mathcal{P},\mathcal{L}$ and their common refinement $\mathcal{P}'.$ Then,

$L(f,\mathcal{P}) \leq L(f,\mathcal{P'}) \leq U(f,\mathcal{P'}) \leq U(f,\mathcal{L}),$

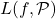
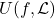
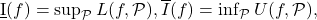
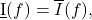
so $L(f,\mathcal{P})$ is bounded above and $U(f,\mathcal{L})$ is bounded below. Take $\underbar{I}(f) = \sup_{\mathcal{P}} L(f,\mathcal{P}), \overline{I}(f) = \inf_{\mathcal{P}} U(f,\mathcal{P}),$ and if $\underbar{I}(f)=\overline{I}(f),$ $f$ is said to be Riemann integrable with

$\overline{I}(f)=\underbar{I}(f) = \int_a^b f(x) dx.$

Proposition:

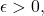
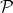
A function is Riemann integrable if and only if for any $\epsilon>0,$ there exists a partition $\mathcal{P}$ such that

$U(f,\mathcal{P}) - L(f,\mathcal{P}) < \epsilon.$

Proposition:

A continuous function $f:[a,b] \to \mathbb{R}$ is Riemann integrable.

Multiple Metrics

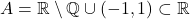
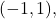
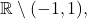
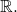
Take $A=\mathbb{R} \setminus \mathbb{Q} \cup (-1,1) \subset \mathbb{R}$ with the usual Euclidean metric. Then, the interior of $A$ is $(-1,1),$ the exterior is empty, boundary is $\mathbb{R} \setminus (-1,1),$ and the closure is $\mathbb{R}.$ Note that

$\mathbb{R} = \text{interior} \cup \text{boundary} \cup \text{exterior}.$

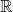
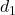
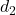
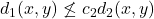
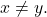
Moreover, the interior of the closure is $\mathbb{R}$ and closure of the interior is $[-1,1],$ so the two operations are not interchangeable. We can define two metrics on this space. Let $d_1$ be the usual Euclidean metric, and let $d_2$ be the discrete metric. Then, the two metrics are not equivalent, since $d_1(x,y) \not \leq c_2 d_2(x,y)$ for any $x \not = y.$ What does an open ball in $A$ look like? What does a closed ball look like?