Analysis Problem of the Day 7

The following problem appears as Problem 5 on the Stanford Fall 2021 Analysis Qual:

Problem 5: Let $H_1, H_2$ be separable Hilbert spaces, and let $A: H_1 \to H_2, B: H_2 \to H_1$ be bounded operators such that $BA = I - E,$ wherer $E$ is a compact operator.

Show that 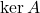$\ker A$ is finite-dimensional and 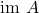$\text{im }A$ is closed in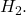 $H_2.$
Give an example of 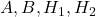$A, B, H_1, H_2$ such that 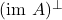$(\text{im }A)^\perp$ is infinite-dimensional.
Show that if 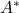$A^*$ is injective, then $A$ is surjective.

Solution: This problem is a classical functional analysis problem. For part a), notice that

$BA|_{\ker A} = (I-E)|_{\ker A} = 0,$

i.e. $I|_{\ker A} = E|_{\ker A}.$ The restriction of a compact operator to any subspace is also compact, and one of the main results of the theory of Banach spaces is that the identity operator is compact if and only if the space is finite-dimensional. Thus, since $I|_{\ker A}$ is compact, $\ker A$ is finite-dimensional.

To show that $\text{im }A$ is closed in $H_2,$ we use the classification of injective operators with closed range as precisely those that are bounded below. Note that we may assume that $A$ is injective by passing to the quotient subspace $H_1 / \ker A.$ We also have use the fact that compact operators can be arbitrarily approximated by finite rank operators. For a finite-rank operator $F$ such that $\|F-E\|<\epsilon$ and any $x \in \ker F,$ one has

$\|B\|\|Ax\| \geq \|BAx\| = \|(I-E)x\| = \|(I-F+F-E)x\| \geq (1-\epsilon)\|x\|.$

This implies that $A$ is bounded below on $\ker F,$ so it has closed range on $\ker F.$ On the other hand, $A((\ker F)^\perp)$ is finite-dimensional since $(\ker F)^\perp = \text{im }F^*$ is finite-dimensional (as finite-rank operators are closed under taking adjoints). Thus, $\text{im }A = A(\ker(F))+A(\ker(F)^\perp)$ is closed.

For b), the first example that should come to mind when working with operators over infinite-dimensional Hilbert spaces is that of $H_1=H_2=l^2.$ From this, we can easily come up with such operators $A$ and $B$ : for instance, $A(a_1,a_2,...) = (0,a_1,0,a_2,...)$ and $B(a_1,a_2,...) = (a_2,a_4,...).$ Then, $BA = I = I - 0,$ where $0$ is trivially a compact operator, and $(\text{im }A)^\perp$ is the subspace of all odd-indexed terms of $l^2,$ which is clearly infinite dimensional.

Part c) is then immediate from the orthogonality relation $(\ker A^*)^\perp = \overline{\text{im }A}$ and the fact that $A$ has closed range, which was proved in a).

Remark: Part a) of this problem essentially reproduces the proof of Atkinson’s theorem, which states that an operator $A$ is Fredholm (i.e. has finite-dimensional kernel and cokernel) if and only if there exists an operator $B$ such that $I-AB$ and $I-BA$ are compact.

Leave a Reply Cancel reply