Today’s problem is a nice result about smooth non-analytic functions known as Borel’s Theorem.
Problem: Let ![]() be any sequence of real numbers. Show that there exists a smooth function
be any sequence of real numbers. Show that there exists a smooth function ![]() such that
such that ![]()
Solution: The naive approach to this problem (which ignores any convergence issues) would be to set ![]() However, as we are aware from the theory of analytic functions, this power series has a positive radius of convergence only if
However, as we are aware from the theory of analytic functions, this power series has a positive radius of convergence only if ![]() The key point in this problem is that we are working over the category of smooth functions, not real analytic ones. We will modify our naive approach by doing a classic trick – introducing a smooth test function
The key point in this problem is that we are working over the category of smooth functions, not real analytic ones. We will modify our naive approach by doing a classic trick – introducing a smooth test function ![]() that equals 1 in a small neighborhood of 0 and vanishes for, say,
that equals 1 in a small neighborhood of 0 and vanishes for, say, ![]() Then, if we define
Then, if we define
![]()
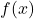 is clearly defined at
is clearly defined at 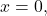 and for
and for  the sum is finite since
the sum is finite since  for large enough
for large enough 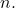 Thus,
Thus, 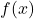 is defined pointwise everywhere.
is defined pointwise everywhere.- In fact, on any compact interval
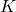 avoiding the origin, the sum is finite and therefore (since
avoiding the origin, the sum is finite and therefore (since 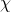 is smooth) defines a smooth function
is smooth) defines a smooth function 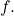 This means that
This means that 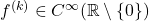 for all
for all 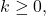 and in fact, one may differentiate the power series for
and in fact, one may differentiate the power series for  term-by-term.
term-by-term. - One may check that
where we switch the order of the limit and infinite sum by an application of the dominated convergence theorem.![Rendered by QuickLaTeX.com \[\lim_{x \to 0} f^{(k)}(x) = \lim_{x \to 0} \sum_{n=0}^\infty a_n \partial_x^k(x^n \chi(nx)) = \sum_{n=0}^\infty a_n \partial_x^k(x^n \chi(nx))|_{x=0} = a_n,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-978773ccc7544a12565a3fa61cd331c2_l3.png)
- Thus, if one defines
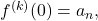 this extends
this extends  to a smooth function satisfying the required properties.
to a smooth function satisfying the required properties.
Remark: Notice that ![]() in general cannot be analytic at 0, since if
in general cannot be analytic at 0, since if ![]() the Taylor series would have a zero radius of convergence.
the Taylor series would have a zero radius of convergence.