Easy:
- Find the radius of convergence of the power series
![Rendered by QuickLaTeX.com \[\sum_{n=1}^\infty \frac{n(x+2)^n}{5^{n-1}}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-14479a14683ec8ec338140bb46b78d62_l3.png)
- Provide an example of a real power series
 with radius of convergence
with radius of convergence 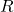 that converges at
that converges at  but diverges at the endpoint
but diverges at the endpoint 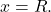
- Let
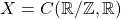 be the space of continuous periodic functions on
be the space of continuous periodic functions on ![Rendered by QuickLaTeX.com [0,1].](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-fe398ab3182eef80acc301bd41f995f8_l3.png) Define the
Define the 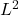 norm on
norm on 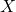 to be
to be
Show that this is indeed a norm on![Rendered by QuickLaTeX.com \[\|f\|_{L^2} = \left(\int_0^1 |f(x)|^2 dx\right)^{\frac{1}{2}}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-97db567acf1c745526d7a0377bc9c8d1_l3.png)
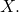 Conclude that the
Conclude that the 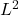 metric on
metric on 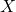 is
is ![Rendered by QuickLaTeX.com \[d(f,g)_{L^2}= \left(\int_0^1|f(x)-g(x)|^2dx \right)^{\frac{1}{2}}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-e311cd84fb5aa956349db9896d1a48fa_l3.png)
- Show that if
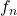 converges to
converges to 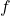 uniformly,
uniformly, 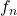 converges to
converges to 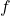 in
in 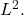
Proof:
By using the root test, we obtain ![]()
Proof:
Take ![]()
Proof:
Indeed ![Rendered by QuickLaTeX.com \[\|f\|_{L^2} = \left(\int_0^1 |f(x)|^2 dx \right)^{\frac{1}{2}} \geq \left(\int_{x-\delta}^{x+\delta} |f(x)|^2 dx\right)^{\frac{1}{2}} \geq \left(\frac{|f(x)|}{2}\right)^2 (2\delta) > 0,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-4a7d2ad2935e9b3c0e67ec77d8816d35_l3.png)
![Rendered by QuickLaTeX.com \[\int_0^1|f(x)g(x)| \leq \sqrt{\int_0^1|f(x)|^2dx}\sqrt{\int_0^1 |g(x)|^2dx},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-65f5dc7966e4423800e597c86ed00891_l3.png)

![]()
Proof:
Indeed, whenever ![Rendered by QuickLaTeX.com \[\|f_n-f\|_{L^2} = \left(\int_{0}^1 |f_n-f|^2\right)^{\frac{1}{2}} \leq \epsilon,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-688a5f8566eb9814ef8868cf7de55095_l3.png)
Medium:
- If
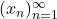 is a sequence of real numbers,
is a sequence of real numbers, 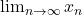 exists if and only if
exists if and only if 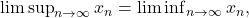 in which case
in which case
![Rendered by QuickLaTeX.com \[\limsup_{n \to \infty} x_n = \liminf_{n \to \infty} x_n = \lim_{n \to \infty} x_n.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5128ff8330e2d6b82e87ef4572a9c289_l3.png)
- (Ratio Test) The radius of convergence of
 is
is 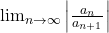 if the value of the limit exists.
if the value of the limit exists. - Show that if
is a real power series with radius of convergence![Rendered by QuickLaTeX.com \[f(x) = \sum_{n=0}^\infty a_n x^n\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-1e35c08bb7f1653603702de8eb0099f2_l3.png)
 then
then 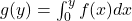 is differentiable on
is differentiable on 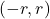 and
and 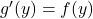 for all
for all 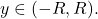 Moreover, show that
Moreover, show that ![Rendered by QuickLaTeX.com \[g(y) = \sum_{n=0}^\infty \frac{a_n}{n+1} y^{n+1}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-cb1bc842ade88c1e20d52522a6c3e78c_l3.png)
Proof:
If ![]()
![]()
Proof:
Note that by the ratio test for series, the series above converges wheneverProof:
Note that since ![Rendered by QuickLaTeX.com \[\frac{g(y+h)-g(y)}{h} - f(y) = \frac{\int_0^{y+h} f(x) dx - \int_0^y f(x) dx} {h} - f(y) = \frac{1}{h}\int_y^{y+h} f(x) - f(y)dx \leq \frac{1}{h} \epsilon = \epsilon,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-2549e10f5800aee190661d0baae05c80_l3.png)
![]()
Challenging:
- Find the Fourier transform of

- Prove Bessel’s inequality: for
 and any
and any 
![Rendered by QuickLaTeX.com \[\sum_{n=1}^N |\langle f, e_n \rangle|^2 \leq \|f\|^2_{L^2}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-3dac3123438487f6d214f1e6c4d43db8_l3.png)
Proof:
Using the identity ![]()
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \mathcal{F}(\sin 2 \pi x)(n) & = \int_0^1 \frac{e^{2\pi i x} - e^{-2\pi i x}}{2i} e^{-2\pi i n x} dx = \int_0^1 \frac{e^{2\pi i x(1-n)} -e^{-2\pi i x (n+1)}}{2i} dx \\ & = \left[\frac{e^{2\pi i x(1-n)}}{2i(2\pi i)(1-n)}\right]^1_0-\left[\frac{e^{-2\pi i x (n+1)}}{2i(-2\pi i (n+1))}\right]^1_0 = \frac{e^{2\pi i (1-n)}-1}{4\pi (n-1)}-\frac{e^{-2\pi i (n+1)}-1}{4\pi (n+1)}. \end{split} \end{equation*}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-553f8e46ac2543d621596c4cb6d8a473_l3.png)
Proof:
Let ![Rendered by QuickLaTeX.com \[\|x\|^2= \|x-y\|^2 + \|y\|^2 \geq \|y\|^2= \sum_{n=1}^N |\langle f, e_n \rangle|^2.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-262aaf4094414c18f96ef5c555bf9e00_l3.png)