Today’s problem appeared as Problem 3 on the UCLA Fall 2009 Analysis Qual:
Problem 3. Let ![Rendered by QuickLaTeX.com f: [0,1] \to \mathbb{R}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-1d03c0804499cc19267ce8daadb52e7b_l3.png) be continuous with
be continuous with ![Rendered by QuickLaTeX.com \min_{x \in [0,1]} f(x) =0,](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b5eb754f58b32228c636e09b946e7245_l3.png) and suppose that for all
and suppose that for all 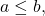
![Rendered by QuickLaTeX.com \[\int_a^b f(x)-(\min_{t \in [a,b]} f(t)) dx \leq \frac12 |b-a|.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-5274ce853591684c3f3da019a5fe43fa_l3.png)
a) Show that for all 
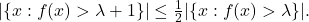
b) Prove that for 
![Rendered by QuickLaTeX.com \[\int_0^1 c^{f(x)} dx \leq \frac{100}{2-c}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-492dc34fd6d48b5acaeb92a9d5cb79a4_l3.png)
Solution: a) Multiplying by 2 on both sides and using 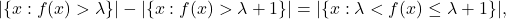 we note that it suffices to prove
we note that it suffices to prove
![Rendered by QuickLaTeX.com \[|\{x:f(x) > \lambda+1\}| \leq |\{x: \lambda < f(x) \leq \lambda+1\}|\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-4ef19e11cc7ce5f04864fd3173e9c3bd_l3.png)
for all
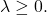
Since

is continuous, note that
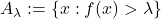
is open for all

Now, take any interval
![Rendered by QuickLaTeX.com [a,b] \subset A_\lambda](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-0d3d0be5bdc8e0f3b2edfcf5f07a03b6_l3.png)
and apply the given condition to obtain
![Rendered by QuickLaTeX.com \[\int_a^b f(x)-\lambda dx \leq \int_a^b f(x) - \min_{[a,b]} f(t) dx \leq \frac12 |b-a|,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-d7fb6c39667569de8d9ec42b17fda539_l3.png)
i.e.
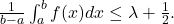
Thus, we conclude that the averages of

on intervals in
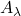
are at most
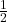
above

By the definition of the average, this implies that
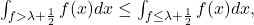
so that
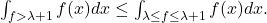
We now apply Chebyshev’s inequality to obtain the desired result. Indeed, since

is non-negative,
![Rendered by QuickLaTeX.com \[|\{x:f(x)>\lambda+1\}| \leq \frac{\int_{f>\lambda+1} f(x)dx}{\lambda+1} \leq \frac{\int_{\lambda \leq f < \lambda+1} f(x)dx}{\lambda+1} \leq |\{x: \lambda \leq f < \lambda+1\}|,\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ebe13f1dbe520070b20434262dcc54b4_l3.png)
as desired.
b) We multiply by the denominator on both sides and apply the layer-cake decomposition to obtain
![Rendered by QuickLaTeX.com \[\int_0^\infty 2|\{x:c^{f(x)}>\lambda\}|-|\{x:c^{f(x)+1}>\lambda\}| dx=\int_0^\infty 2\left|\left\{x:f(x)>\frac{\log \lambda}{\log c}\right\}\right|-\left|\left\{x:f(x)>\frac{\log \lambda}{\log c}-1\right\}\right| dx.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-c69b325dfbb4f3aec77292876a502f83_l3.png)
Now, for
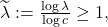
the claim in (a) gives us that the integrand is bounded above by 0. But note that this holds only if
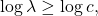
i.e.
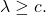
We can thus conclude that
![Rendered by QuickLaTeX.com \[\int_0^1 c^{f(x)}dx \leq \int_0^c 2|\{x:c^{f(x)}>\lambda\}|-|\{x:c^{f(x)}>\lambda+1\}| d\lambda \leq 4.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-c7adc52e5a29ad5b2f3f85305da71245_l3.png)
Thus,
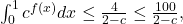
as claimed.
![]() be continuous with
be continuous with ![]() and suppose that for all
and suppose that for all ![]()
![]()
![]()
![]()
![]()
![]()
![]() we note that it suffices to prove
we note that it suffices to prove ![]()
![]()
![]()
![]()
![]()