Today’s problem is Problem 10 on the UCLA Spring 2023 Analysis Qual:
Problem 10. A function of the form
![Rendered by QuickLaTeX.com \[B(z) = \lambda \prod_{i=1}^n \frac{z-a_j}{1-\overline{a_j} z}, \quad a_j \in \mathbb{D}, |\lambda|=1\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-1b1cbc35363d40a357984da78093487c_l3.png)
is called a
Blaschke product of degree n. Show that for
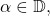
![Rendered by QuickLaTeX.com \[z \to \frac{B(z)+\alpha}{1+\overline{\alpha} B(z)}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-b3a1b5cee2f4523b2f5e7b95e3538a07_l3.png)
is a Blaschke product of degree
Solution: Notice that the map
![Rendered by QuickLaTeX.com \[g: z \to \frac{B(z)+\alpha}{1+\overline{\alpha} B(z)}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-9b94020c2a62bfafd5244a89a2a1f2e1_l3.png)
is given by
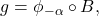
where
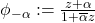
is the automorphism of the unit disc sending
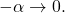
In particular, the images of the zeros
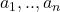
of
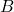
under
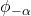
are
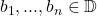
(up to multiplicity). Moreover, each factor of the Blaschke product satisfies
![Rendered by QuickLaTeX.com \[\left|\frac{z-a_j}{1-\overline{a_j} z}\right| = 1\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-ef9bc0515a55c3a16b5ed8e6d87ac52d_l3.png)
when
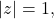
so therefore this also holds for the product
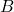
and correspondingly also the composition
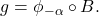
Now, define
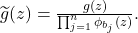
Then,
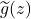
is a holomorphic function on the unit disc with no zeros inside
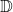
and
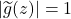
when
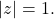
By the maximum modulus principle applied to
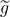
and
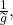
we conclude that
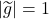
on
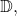
i.e.
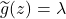
is constant with
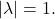
This immediately implies that
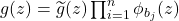
is a Blaschke product of degree
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()