Today’s quite intimidating problem appeared as Problem 5 on the UCLA Spring 2023 Analysis Qual:
Problem 5. Let  be the standard basis for
be the standard basis for 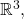 and let
and let 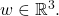
a) Show that there is no 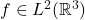 satisfying
satisfying
![Rendered by QuickLaTeX.com \[f(x) = \frac16 \sum_{j=1}^3 (f(x+e_j)+f(x-e_j)) +e^{iw \cdot x - |x|^2/2}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-3b055ec8e5ee96d38ae69721a44bf93c_l3.png)
a.e.
b) Show that for every 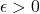 there exists
there exists 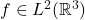 such that
such that
![Rendered by QuickLaTeX.com \[\left\|f(x)-\left(\frac16 \sum_{j=1}^3 (f(x+e_j)+f(x-e_j)) +e^{iw \cdot x - |x|^2/2}\right)\right\|_2^2 < \epsilon.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-fad55a6dbd430e66fde5138782953185_l3.png)
Solution: a) The presence of a complex exponential, a Gaussian, and the fact that we are working over 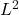 highly suggests that this problem is related to the Fourier transform. Thus, let’s take the Fourier transform on both sides to get
highly suggests that this problem is related to the Fourier transform. Thus, let’s take the Fourier transform on both sides to get
![Rendered by QuickLaTeX.com \[\widehat{f}(\xi) = \frac16 \sum_{j=1}^3 \widehat{f}(\xi) (e^{i e_j \cdot \xi}+e^{-i e_j \cdot \xi}) + e^{-|\xi -w|^2/2},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-37f4ac5a95b4b29e5ff55388dcb42e5d_l3.png)
where we use the fact that the Fourier transform of a Gaussian is a Gaussian and translation corresponds to a phase shift on the frequency side. Simplifying and solving for
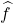
yields
![Rendered by QuickLaTeX.com \[\widehat{f}(\xi) = \frac{e^{-|\xi-w|^2/2}}{1-\frac13\sum_{j=1}^3 \cos (\xi_i)}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-1e87ac4cade0d411d181e4bb64f83b72_l3.png)
Notice that the right hand side blows up whenever
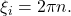
To understand how fast this blow up occurs, we Taylor expand by using
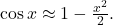
Then, the denominator simplifies as
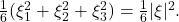
On
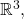
integrating in spherical coordinates yields a Jacobian factor proportional to
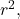
so since the Gaussian is bounded near the origin, the
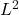
norm of
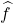
is bounded below by
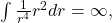
i.e.
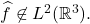
By Plancherel’s theorem, this implies that
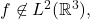
so no

satisfying such conditions can exist.
b) From the above discussion, the issue with 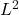 integrability clearly occurs precisely at the lattice points
integrability clearly occurs precisely at the lattice points 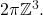 To remedy this, we thus may modify
To remedy this, we thus may modify 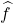 in a small neighborhood of those lattice points. For small enough
in a small neighborhood of those lattice points. For small enough 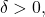 pick balls of radii
pick balls of radii 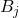 of radii
of radii ![Rendered by QuickLaTeX.com \frac{\delta}{\sqrt[3]{\frac43\pi}2^{\frac{j}{3}}}](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-162aad44112087adfe0c5ac8d9c1e319_l3.png) centered at the lattice points so that
centered at the lattice points so that  (this can be done by absolute continuity). Then, set
(this can be done by absolute continuity). Then, set 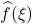 to be
to be
![Rendered by QuickLaTeX.com \[\widehat{f}(\xi) := \frac{e^{-|\xi-w|^2/2}}{1-\frac13\sum_{j=1}^3 \cos (\xi_i)}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-6ec06f3e3ea2142b0817bf9df72b0cef_l3.png)
outside of those balls and some fixed
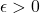
on
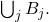
Note that
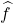
has finite
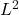
norm on

rougly bounded by
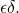
Moreover,
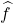
has finite
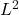
norm on
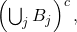
since the Gaussian is in
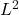
and near the lattice points,
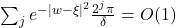
(since
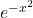
decays faster than the growth of
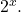
) Thus,
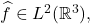
so by Plancherel’s,
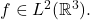
Finally, by shrinking
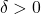
if necessary,
![Rendered by QuickLaTeX.com \[\widehat{f}(\xi) - \left(\frac16 \sum_{j=1}^3 \widehat{f}(\xi) (e^{i e_j \cdot \xi}+e^{-i e_j \cdot \xi}) + e^{-|\xi -w|^2/2}\right)\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-febeadd0d3a2fedbe8e55a8dc96808ca_l3.png)
has
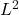
norm less than

since the function vanishes on
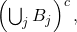
while on all of the balls,
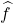
contributes at most a constant multiple of
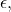
and so does the Gaussian. Thus, the inverse Fourier transform

of
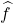
as constructed satisfies the statement of the problem.
![]() be the standard basis for
be the standard basis for ![]() and let
and let ![]()
![]() satisfying
satisfying ![Rendered by QuickLaTeX.com \[f(x) = \frac16 \sum_{j=1}^3 (f(x+e_j)+f(x-e_j)) +e^{iw \cdot x - |x|^2/2}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-3b055ec8e5ee96d38ae69721a44bf93c_l3.png)
![]() there exists
there exists ![]() such that
such that ![Rendered by QuickLaTeX.com \[\left\|f(x)-\left(\frac16 \sum_{j=1}^3 (f(x+e_j)+f(x-e_j)) +e^{iw \cdot x - |x|^2/2}\right)\right\|_2^2 < \epsilon.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-fad55a6dbd430e66fde5138782953185_l3.png)
![]() highly suggests that this problem is related to the Fourier transform. Thus, let’s take the Fourier transform on both sides to get
highly suggests that this problem is related to the Fourier transform. Thus, let’s take the Fourier transform on both sides to get ![Rendered by QuickLaTeX.com \[\widehat{f}(\xi) = \frac16 \sum_{j=1}^3 \widehat{f}(\xi) (e^{i e_j \cdot \xi}+e^{-i e_j \cdot \xi}) + e^{-|\xi -w|^2/2},\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-37f4ac5a95b4b29e5ff55388dcb42e5d_l3.png)
![Rendered by QuickLaTeX.com \[\widehat{f}(\xi) = \frac{e^{-|\xi-w|^2/2}}{1-\frac13\sum_{j=1}^3 \cos (\xi_i)}.\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-1e87ac4cade0d411d181e4bb64f83b72_l3.png)
![]() integrability clearly occurs precisely at the lattice points
integrability clearly occurs precisely at the lattice points ![]() To remedy this, we thus may modify
To remedy this, we thus may modify ![]() in a small neighborhood of those lattice points. For small enough
in a small neighborhood of those lattice points. For small enough ![]() pick balls of radii
pick balls of radii ![]() of radii
of radii ![]() centered at the lattice points so that
centered at the lattice points so that ![]() (this can be done by absolute continuity). Then, set
(this can be done by absolute continuity). Then, set ![]() to be
to be ![Rendered by QuickLaTeX.com \[\widehat{f}(\xi) := \frac{e^{-|\xi-w|^2/2}}{1-\frac13\sum_{j=1}^3 \cos (\xi_i)}\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-6ec06f3e3ea2142b0817bf9df72b0cef_l3.png)
![Rendered by QuickLaTeX.com \[\widehat{f}(\xi) - \left(\frac16 \sum_{j=1}^3 \widehat{f}(\xi) (e^{i e_j \cdot \xi}+e^{-i e_j \cdot \xi}) + e^{-|\xi -w|^2/2}\right)\]](https://www.stepanmalkov.com/wp-content/ql-cache/quicklatex.com-febeadd0d3a2fedbe8e55a8dc96808ca_l3.png)